1.3.4. Примеры решения задач по теме «Обратная матрица»
Задача 1.
Найти обратную матрицу для матрицы
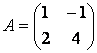
И проверить выполнение условий А А-1 = А-1А = Е.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Убедимся, что матрица А – невырожденная. ΔА = 1·4 - 2·(-1) ≠ 0, следовательно, А-1 существует.
Вычислим алгебраические дополнения к элементам А:
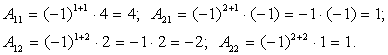
Применим способ вычисления обратной матрицы:
 .
.
|
Не забудьте, что обратная матрица образована из алгебраических дополнений к элементам Транспонированной матрицы! |
Найдем произведения А А-1 и А-1А:
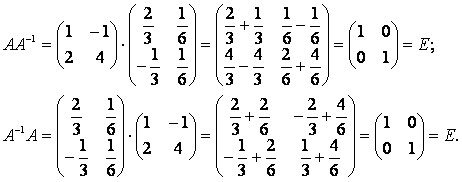
Таким образом, найденная матрица А-1 отвечает определению обратной матрицы.
Ответ: 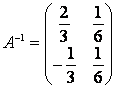 .
.
Задача 2.
Найти обратную матрицу для матрицы
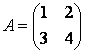 .
.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
![]()
Следовательно, матрица А невырожденная, и обратная матрица существует.
Вычислим алгебраические дополнения к элементам матрицы А:
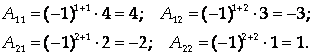
Обратная матрица имеет вид:

Ответ: 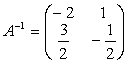 .
.
Задача 3.
Найти обратную матрицу для матрицы
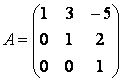 .
.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
Вычислим определитель матрицы А разложением по первому столбцу:
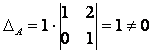 .
.
Следовательно, обратная матрица для матрицы А существует.
Найдем алгебраические дополнения к элементам матрицы А:
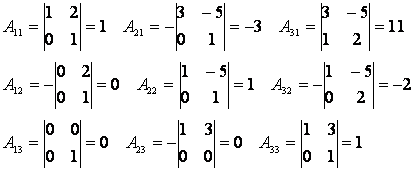
Значит,

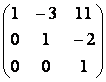 .
.
Ответ:  .
.
Задача 4.
Найти обратную матрицу для матрицы
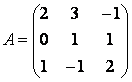 .
.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
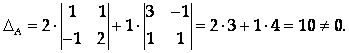

 .
.
Ответ: 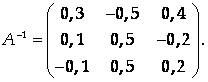
Задача 5.
При каких X, Y, Z матрица
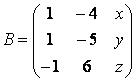
Является обратной к матрице

Указание
Необходимым условием того, что В = А-1, является требование АВ = Е.
Решение
Проверим невырожденность матрицы А:
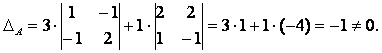
Необходимым условием того, что В = А-1, является требование АВ = Е.
Найдем АВ:
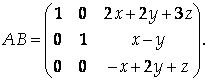
Для того, чтобы выполнялось условие АВ = Е, X, Y, Z должны быть решением системы уравнений
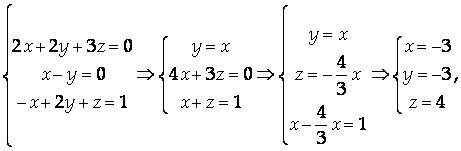

Проверим, будет ли равно единичной матрице произведение ВА:
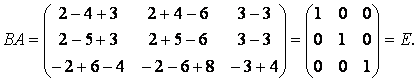
Значит, при найденных значениях X, Y, Z В = А-1.
Ответ: X = -3, Y = -3, Z = 4.
| < Предыдущая | Следующая > |
|---|