13.Ортонормированный базис. Процесс ортогонализации по Гильберту — Шмидту
Определение:
Базис ![]() в пространстве
в пространстве ![]() называется ортонормированным (ОНБ), если
называется ортонормированным (ОНБ), если ![]()
![]()
Здесь![]() если
если ![]() и
и ![]() ;
; ![]() . Корректность последнего определения следуетиз теоремы
. Корректность последнего определения следуетиз теоремы
Теорема:
Система попарно ортогональныхи ненулевых элементов ![]() является л. н.з.
является л. н.з.
Доказательство: Выясним условия выполнения равенства ![]() θ
θ
Для этого обе части данного равенства умножаем скалярно на один из элементов данной системы
![]()
![]() , здесь
, здесь ![]()
Отсюда следует, что ![]() , но т. к.
, но т. к. ![]() θ, то
θ, то ![]() . В силу произвольности выбора эл-та
. В силу произвольности выбора эл-та ![]() , получаем, что
, получаем, что ![]() ─ л. н.з. #
─ л. н.з. #
Итак, для ОНБ эл-ты матрицы Грама равны ![]() , т. е.
, т. е. ![]() (здесь
(здесь ![]() ─ единичная матрица). Отсюда
─ единичная матрица). Отсюда
![]() в ОНБ евклидова пространства
в ОНБ евклидова пространства ![]() :
:
![]() в ОНБ унитарного пространства
в ОНБ унитарного пространства ![]() .
.
Теорема Гильберта-Шмидта (об ортогонализации базиса):
Во всяком ![]() -мерном унитарном (евклиловом) пространстве существует ОНБ.
-мерном унитарном (евклиловом) пространстве существует ОНБ.
Доказательство: ![]()
![]() произвольный базис в пространстве
произвольный базис в пространстве ![]() (
(![]() или
или ![]() ). Докажем, что можно построить
). Докажем, что можно построить ![]() в-в
в-в ![]() , которые линейно выражаются через
, которые линейно выражаются через ![]() и образуют ОНБ. Будем доказывать методом матматической индукции.
и образуют ОНБ. Будем доказывать методом матматической индукции.
1) Если имеется один в-р ![]() , то для построения в-ра
, то для построения в-ра ![]() с нормой, равной единице достаточно нормировать в-р
с нормой, равной единице достаточно нормировать в-р ![]() :
:![]()
2) теперь предположим, что утверждение доказано для ![]() в-в
в-в ![]() , которые линейно выражаются через в-ры
, которые линейно выражаются через в-ры ![]() , являются единичными и попарно ортогональными.
, являются единичными и попарно ортогональными.
3) Рассмотрим в-р ![]() , (*)
, (*)
Здесь ![]() , т. к. в-ры
, т. к. в-ры ![]() линейно выражаются через в-ры
линейно выражаются через в-ры ![]() и если бы
и если бы ![]() θ, то получили бы линейную зависимость базисных в-в
θ, то получили бы линейную зависимость базисных в-в ![]() , что невозможно.
, что невозможно.
Выберем ![]() так, чтобы
так, чтобы ![]() ,
, ![]() .
.
Для этого рав-во (*) умножаем скалярно на ![]() , получаем
, получаем
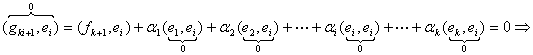
![]()
Таким образом, если ![]() , то можно положить,
, то можно положить,
![]() . Тем самым построен
. Тем самым построен ![]() -ый в-р
-ый в-р ![]() #
#
Замечание: Алгоритм построен ОНБ по формулам ![]() , где
, где ![]() называется процессом ортогонализации Гильберта-Шмидта
называется процессом ортогонализации Гильберта-Шмидта
| < Предыдущая | Следующая > |
|---|