06. Перестановки
1) Рассмотрим непустое конечное множество ![]() ,
, ![]() .
.
Из ![]() элементов этого множества сформируем различные выборки Без возвращения и с учётом порядка извлечённых элементов. Получаемые при таких условиях упорядоченные выборки называются Перестановками из
элементов этого множества сформируем различные выборки Без возвращения и с учётом порядка извлечённых элементов. Получаемые при таких условиях упорядоченные выборки называются Перестановками из ![]() элементов.
элементов.
Число перестановок для данного мноежества обозначается ![]() и вычисляется по формуле
и вычисляется по формуле ![]() .
.
Пример. Три студента сдают экзамен по высшей математике. Сколько всего существует вариантов распределения оценок, если известно, что все они сдали экзамен и получили разные оценки?
Решение. По условию задачи все три студента экзамен сдали. Поэтому данное множество оценок ![]() ,
, ![]() ,
, ![]() . Для ответа на вопрос задачи надо составить комбинаторные конфигурации из трёх элементов множества
. Для ответа на вопрос задачи надо составить комбинаторные конфигурации из трёх элементов множества![]() без возвращения и с учётом порядка извлечённых элементов. Число вариантов распределения оценок в соответствии с заданными условиями равно числу перестановок из 3 элементов:
без возвращения и с учётом порядка извлечённых элементов. Число вариантов распределения оценок в соответствии с заданными условиями равно числу перестановок из 3 элементов: ![]() .□
.□
2) Рассмотрим последовательность ![]() элементов, содержащую
элементов, содержащую ![]() элементов
элементов ![]() ,
, ![]() элементов
элементов ![]() , …,
, …, ![]() элементов
элементов ![]() . Элементы
. Элементы ![]() различны,
различны, ![]() . Из
. Из ![]() элементов этой последовательности сформируем различные выборки Без возвращения с учётом порядка извлечённых элементов. Различные перестановки элементов данной последовательности называются Перестановками с повторениями из
элементов этой последовательности сформируем различные выборки Без возвращения с учётом порядка извлечённых элементов. Различные перестановки элементов данной последовательности называются Перестановками с повторениями из ![]() элементов.
элементов.
Число таких перестановок с повторениями для данной последовательности обозначается ![]() или
или ![]() и вычисляется по формуле
и вычисляется по формуле 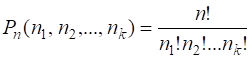 .
.
Пример. Студент Петров помнит, что телефонный номер куратора группы начинается с семёрки и содержит три единицы и две тройки. Расположение пяти последних цифр студент забыл. Сколько попыток потребуется Петрову, чтобы точно дозвониться куратору? Предполагается, что каждый абонент отвечает при первом вызове.
Решение. По условию задачи данная последовательность состоит из цифр 1, 1, 1, 3, 3, ![]() ,
, ![]() ,
, ![]() . Расположение цифры 7 в номере телефона известно, поэтому она не входит в последовательность. Для ответа на вопрос задачи надо найти число перестановок с повторениями из пяти элементов
. Расположение цифры 7 в номере телефона известно, поэтому она не входит в последовательность. Для ответа на вопрос задачи надо найти число перестановок с повторениями из пяти элементов 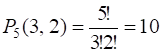 .□
.□
Задачи и упражнения.
6.1. Вычислите 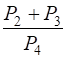 .
.
6.2. Сколько букв «алфавита» можно составить из пяти символов в каждой его букве, если три символа – единицы и два символа - нули?
6.3. Сколько различных семибуквенных слов (не все они имеют смысл) можно составить из букв слова «БАРАБАН»?
6.4. Сколько существует способов поставить Иванова, Петрова и еще 8 человек в очередь друг за другом так, чтобы Иванов и Петров стояли рядом?
6.5. Решите уравнение 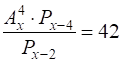 .
.
| < Предыдущая | Следующая > |
|---|