07.2. Второй замечательный предел
Если натуральное число 1 умножить на себя N раз, то в результате получим 1, даже если N будет стремиться к бесконечности.
Если число, меньше 1,скажем число 0,9 возведем в восьмую степень (на калькуляторе наберем 0,9, трижды нажмем клавиши «Х» «=»), то получим 0,98=0,43. Легко проверить, что 0,9n стремится к нулю, если N→∞. Точно также число большее 1, скажем число 1,18=2,14, а (1,1)N→∞, если N→∞. Любое число, меньшее 1, в бесконечной степени дает 0, а большее 1 при возведении в ∞ степень дает ∞. Что будет, если (1 ±a ), где a – бесконечно малая величина, возвести в бесконечно большую степень? Возникает неопределенность вида 1∞. На рис.5 приведен график функции ![]() .
.
Область определения: ![]() .
.
![]() ,
, ![]() .
.
Прямая ![]() является асимптотой этого графика. К ней приближаются обе ветви графика функции при удалении
является асимптотой этого графика. К ней приближаются обе ветви графика функции при удалении ![]() на
на ![]() (вправо) и на
(вправо) и на ![]() (влево).
(влево).
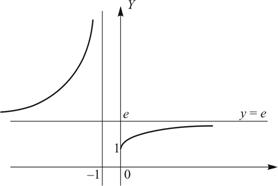
Рисунок 5 – График функции ![]()
Неопределенность │1∞│ раскрывает второй замечательный предел:
![]() ;
;
![]() . (3)
. (3)
Число ![]() – иррациональное и такое же важное в практической жизни, что и число
– иррациональное и такое же важное в практической жизни, что и число ![]() . Его значение с десятью верными знаками после запятой:
. Его значение с десятью верными знаками после запятой: ![]() = 2,71828184… Это число является основанием показательной функции
= 2,71828184… Это число является основанием показательной функции ![]() , а функция
, а функция ![]() , где
, где ![]() некоторая постоянная, описывает многие природные процессы: радиоактивный распад вещества, размножение вируса, вообще образование биологических колоний. С помощью функции
некоторая постоянная, описывает многие природные процессы: радиоактивный распад вещества, размножение вируса, вообще образование биологических колоний. С помощью функции ![]() образуются новые, так называемые гиперболические функции. Это гиперболический синус
образуются новые, так называемые гиперболические функции. Это гиперболический синус ![]() , гиперболический косинус,
, гиперболический косинус, ![]() , гиперболический тангенс
, гиперболический тангенс ![]() и котангенс
и котангенс ![]() . Графики этих функций, а также их определение и некоторые свойства приводятся в приложении I, §1.5., рис. 1.6.
. Графики этих функций, а также их определение и некоторые свойства приводятся в приложении I, §1.5., рис. 1.6.
Кстати, в мире комплексных чисел, а также и функций комплексного переменного гиперболические функции переходят в тригонометрические с таким же названием и наоборот. В нашем реальном мире график косинуса гиперболического описывает дугу равномерно оледеневшего провода провисшего между двумя столбами линии электропередачи.
Логарифмы с основанием ![]() называются натуральными и обозначаются
называются натуральными и обозначаются ![]() . Таким образом,
. Таким образом, ![]() . С помощью второго замечательного предела тоже можно получить эквивалентные функции:
. С помощью второго замечательного предела тоже можно получить эквивалентные функции:
При ![]()
![]()
![]()
![]() .
.
| < Предыдущая | Следующая > |
|---|