27. Числовые функции. Функция, ее свойства и график
Пусть X и Y Некоторые числовые множества ![]()
![]()
Если каждому ![]() по некоторому правилу F ставится в соответствие единственный элемент
по некоторому правилу F ставится в соответствие единственный элемент ![]() то говорят, что Задана функция. Обозначается
то говорят, что Задана функция. Обозначается
![]()
Где Х – аргумент или независимая переменная функции; У – значение функции или зависимая переменная.
Множество Х значений независимой переменной называется Областью определения функции и обозначается ![]() или
или ![]()
Множество всех значений зависимой переменной Y называется Множеством значений функции и обозначается ![]() или
или ![]()
Частное значение функции ![]() при заданном частном значении аргумента
при заданном частном значении аргумента ![]()
![]() обозначается
обозначается ![]()
Отметим особенности отыскания области определения некоторых функций:
1) область определения ![]() дробно-рациональной функции
дробно-рациональной функции
![]()
Где P(X), Q(X) – некоторые многочлены, определяется условием:
![]()
2) если аналитическое выражение функции содержит квадратный корень, т. е. задана функция ![]() то
то
![]()
В случае задания функции формулой ![]() ее область определения
ее область определения ![]() – это ОДЗ выражения
– это ОДЗ выражения ![]()
Графиком функции ![]() называется множество всех точек плоскости с координатами
называется множество всех точек плоскости с координатами ![]() где
где ![]()
Способы задания числовой функции:
1) Табличный – указываются значения переменной Х и соответствующие им значения переменной Y, составляется таблица (можно использовать для записи наблюдений);
|
X |
… |
… |
… |
|
F(X) |
… |
… |
… |
2) Аналитический – указывается область определения функции ![]() и задается формула, по которой каждому значению
и задается формула, по которой каждому значению ![]() ставится в соответствие
ставится в соответствие ![]()
3) Графический – задается график функции.
Свойства функции:
1. Четность и нечетность функции.
Функция ![]() называется Четной, если:
называется Четной, если:
1) ![]() – симметричное множество относительно
– симметричное множество относительно ![]()
2) для любого ![]() выполняется равенство
выполняется равенство ![]()
Функция ![]() называется Нечетной, если:
называется Нечетной, если:
1) ![]() – симметричное множество относительно
– симметричное множество относительно ![]()
2) для любого ![]() выполняется равенство
выполняется равенство ![]()
Если функция ![]() является четной или нечетной, то говорят, что Она обладает свойством четности.
является четной или нечетной, то говорят, что Она обладает свойством четности.
График четной функции симметричен относительно оси ![]() график нечетной – относительно начала координат.
график нечетной – относительно начала координат.
Свойства четных (нечетных) функций:
1) если F и G – четные функции на множестве Х, то функции
![]() – четные функции на Х;
– четные функции на Х;
2) если F и G – нечетные функции на множестве Х, то функции
![]() – нечетные функции на Х;
– нечетные функции на Х;
![]() – четные функции на Х.
– четные функции на Х.
2. Периодичность функции.
Функция ![]() с областью определения
с областью определения ![]() называется Периодической, если существует такое число
называется Периодической, если существует такое число ![]() что для любого значения
что для любого значения ![]() выполняются условия:
выполняются условия:
1) ![]()
2) ![]()
Число Т называется Периодом функции.
Числа ![]() где
где ![]() также будут периодами функции.
также будут периодами функции.
Наименьший из положительных периодов, если он существует, называется Основным периодом.
Значения периодической функции повторяются через период Т. Следовательно, для построения графика данной функции достаточно построить часть графика на любом из промежутков длины Т (из ![]() ), а затем произвести параллельный перенос данной части графика вдоль оси Ох на
), а затем произвести параллельный перенос данной части графика вдоль оси Ох на ![]() .
.
Если функция ![]() – периодическая и имеет период Т, то функция
– периодическая и имеет период Т, то функция ![]() где A, K и
где A, K и ![]() также периодична, причем ее период равен
также периодична, причем ее период равен ![]()
Справедливы утверждения:
1) если ![]() и
и ![]() – периодические функции с общим периодом Т, то функции
– периодические функции с общим периодом Т, то функции ![]() – также периодические, с тем же периодом Т;
– также периодические, с тем же периодом Т;
2) для того, чтобы периодические функции ![]() и
и ![]() с периодами Т1 и Т2 имели общий период Т (число Т должно нацело делиться на Т1 и Т2), необходимо и достаточно, чтобы отношение
с периодами Т1 и Т2 имели общий период Т (число Т должно нацело делиться на Т1 и Т2), необходимо и достаточно, чтобы отношение ![]() было числом рациональным.
было числом рациональным.
3. Монотонность функции.
Пусть Х1, Х2 – произвольные значения из области ![]() функции
функции ![]() такие, что
такие, что ![]()
Если при данном условии выполняется:
![]() то функция называется Возрастающей;
то функция называется Возрастающей;
![]() – Убывающей;
– Убывающей;
![]() – Неубывающей;
– Неубывающей;
![]() – Невозрастающей.
– Невозрастающей.
Возрастающие, убывающие, неубывающие, невозрастающие функции называются Монотонными функциями (возрастающие и убывающие – строго монотонными).
Функция ![]() называется Кусочно-монотонной на множестве Х, если данное множество можно разделить на конечное число промежутков, на каждом из которых функция монотонна.
называется Кусочно-монотонной на множестве Х, если данное множество можно разделить на конечное число промежутков, на каждом из которых функция монотонна.
4. Промежутки знакопостоянства функции. Нули функции.
Числовые промежутки, на которых функция сохраняет свой знак (т. е. ![]() или
или ![]() ), называются Промежутками знакопостоянства.
), называются Промежутками знакопостоянства.
Значения аргумента ![]() при которых функция
при которых функция ![]() называются Нулями функции. Нули функции – это точки пересечения графика функции с осью Ох.
называются Нулями функции. Нули функции – это точки пересечения графика функции с осью Ох.
Пример 1. Найти область определения функции
![]()
![]() (4.1)
(4.1)
Найдем соответствующее ![]() множество точек.
множество точек.
Неравенство ![]() равносильно неравенству
равносильно неравенству
![]()
Решая его, получаем (рис. 4.1):
![]()
![]()
Рис. 4.1
Условие ![]() означает, что
означает, что ![]() т. е.
т. е. ![]()
Приходим к заключению, что
![]() Получаем
Получаем ![]()
Таким образом, система (4.1) равносильна системе
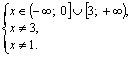
Следовательно, ![]()
Пример 2. Найти множество значений функции
![]()
Решение. Найдем область определения функции
![]()
![]()
![]()
Последнее условие выполняется только для ![]() Вычисляем значение функции в этой точке:
Вычисляем значение функции в этой точке: ![]()
Следовательно, ![]()
Пример 3. Исследовать функцию на четность:
1) ![]() 2)
2) ![]() 3)
3) ![]()
Решение. 1) Замечаем, что функция ![]() имеет
имеет ![]() Следовательно, функция определена на симметричном множестве.
Следовательно, функция определена на симметричном множестве.
Рассмотрим ее значение для –Х:
![]()
Поскольку выполняются оба условия четности функции, заключаем, что функция ![]() – четная.
– четная.
2) Функция ![]() имеет
имеет ![]()
Так как ![]() не является симметричным множеством, второе условие проверять нет необходимости. Эта функция не обладает свойством четности.
не является симметричным множеством, второе условие проверять нет необходимости. Эта функция не обладает свойством четности.
3) Очевидно, что функция ![]() имеет
имеет ![]() т. е. определена на симметричном множестве и для нее справедливо равенство:
т. е. определена на симметричном множестве и для нее справедливо равенство:
![]()
Оба условия нечетности функции выполняются, а потому данная функция является нечетной.
Пример 4. Пусть ![]() где
где ![]() Причем, функция имеет период 2. Построить ее график.
Причем, функция имеет период 2. Построить ее график.
Решение. Построим график данной функции на ![]() (рис. 4.2).
(рис. 4.2).
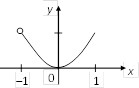
Рис. 4.2
Исходя из определения периодической функции, должно выполняться условие: ![]() где
где ![]()
Строим ее график, продолжая по периоду (рис. 4.3).
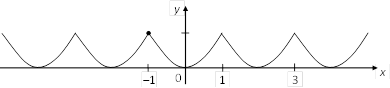
Рис. 4.3
Пример 5. Используя определение монотонной функции, найти значения А, при которых функция ![]() где
где ![]() монотонно возрастает.
монотонно возрастает.
Решение. Пусть![]()
![]() Функция монотонно возрастает, если выполняется условие
Функция монотонно возрастает, если выполняется условие ![]() или
или ![]() Это означает, что
Это означает, что
![]()
Поскольку ![]() последнее неравенство выполняется, если
последнее неравенство выполняется, если ![]() т. е.
т. е. ![]()
Таким образом, функция возрастает для ![]()
Пример 6. Дана функция
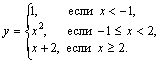
Определить промежутки знакопостоянства функции, нули функции. Построить график данной функции.
Решение. Так как на каждом из данных промежутков аналитические выражения, задающие функцию, определены в каждой точке, следовательно, ![]()
1. Исследуем функцию при ![]() На данном промежутке функция принимает значение, равное 1, т. е. она знакоположительна и нулей функции нет.
На данном промежутке функция принимает значение, равное 1, т. е. она знакоположительна и нулей функции нет.
2. Пусть ![]()
При таком условии функция задается формулой ![]() и
и ![]()
![]() Функция знакоположительна. Здесь она имеет нуль
Функция знакоположительна. Здесь она имеет нуль ![]()
3. Пусть ![]()
Очевидно, что при этом условии ![]() так как
так как ![]() Нулей функции на этом промежутке нет.
Нулей функции на этом промежутке нет.
Построим график:
- если ![]() строим часть прямой линии
строим часть прямой линии ![]()
- если ![]() – часть параболы
– часть параболы ![]()
- если ![]() – часть прямой
– часть прямой ![]()
Получили график заданной функции (рис. 4.4).
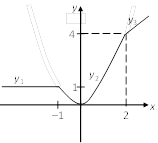
Рис. 4.4
Таким образом, функция знакоположительна ![]() имеет нуль
имеет нуль ![]()
| < Предыдущая | Следующая > |
|---|