4.2. Длина дуги плоской кривой
Предварительно изучите по учебнику Г. М. Фихтен-гольца главу XII, п° п° 199,201, 202. Разберите подробно примеры, решенные в п° 201.
I. Уравнение кривой задано в декартовой системе координат. В теоретическом курсе доказывается, что длина дуги плоской кривой у = f (х) может быть вычислена при помощи определенного интеграла:
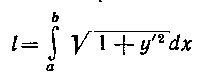
ь
а
ИЛИ
d
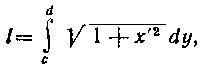
с
где а и b — абсциссы, а с и d — ординаты точек концов данной дуги.
483. Вычислить длину дуги параболы у2 = 4х от точки х = 0 до х = I.
Решение. Для вычисления длины данной дуги воспользуемся второй из данных формул. Заметим, что при х = 0 будет у = 0, а при х = I будет у = + 2.
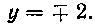
Из уравнения параболы находим, следователь
но,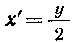
, отсюда
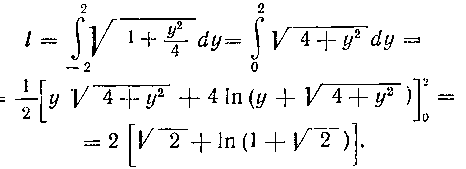
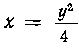
484. Вычислить длину дуги кривей у=\—In cosх от точки M (О, I) до точки N \ 2 J.
Решение. Для вычисления длины дуги воспользуемся первой из данных формул, тогда у = I — Incosx,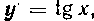 
, следовательно,
до точки В
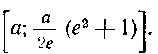
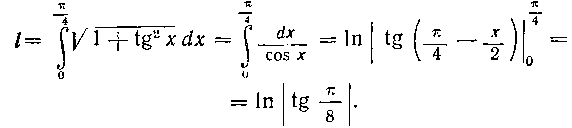
485. Вычислить длину дуги цепной линии
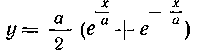
от точки А
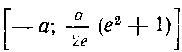
488. Найти длину дуги OA параболы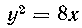
, где
0(0; 0), А (2; 4). Вычисление провести двумя способами.
487. Спрямить кривую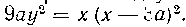
488. Вычислить длину дуги кривой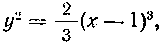
заключенной внутри параболы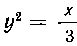
489. Найти длину дуги астроиды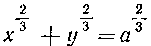
490. Найти длину дуги полукубической параболы
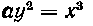Между точками х = 0 и х = 2а.
491. Найти длину дуги кривойIn у от точки у = I до точки у = 2.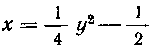
492. Найти длину дуги кривой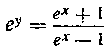
От х = а
2. Кривые заданы параметрическими уравнениями или в полярной системе координат. Как известно из теоретического курса, длина дуги кривой, заданной параметрическими уравнениями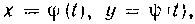
Где функци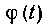и
и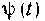
Непрерывны вместесо своими производными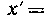
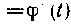И
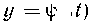На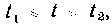
Вычисляется по формуле:
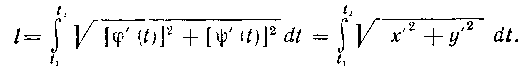
493. Вычислить длину одной арки циклоиды: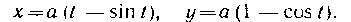 
Решение. Найдем производные по аргументу t:
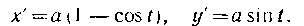
Следовательно,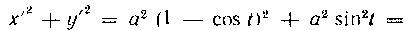
. Так как параметр t изменяйся от 0 до 2я
и в этом промежутке функции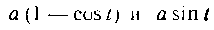
Не*
прерывны, то, сл чьвательно,
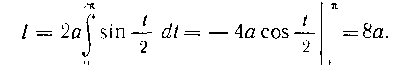
494. Вычислить длину дуги кривой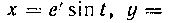
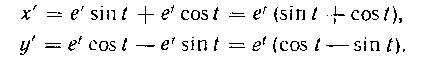
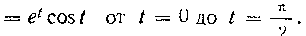
Решение. Вычислим производные по аргументу t:
В промежутке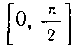
Эти функции непрерывны (как сум
мы произведений непрерывных функций).
Вычислим сумму:
495. Найти длину петли кривей: X=I21 y~t--- /3.
3
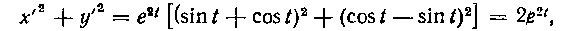
x'z y>2 _ eit J(sjn I _j_ cos IY _|_ (cos I _ sin f)2j _ 2^2
следовательно,
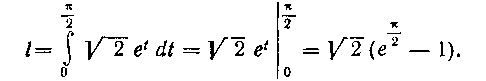
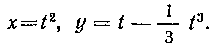
Решение. Найдем точки пересечения кривой с осью Ох:
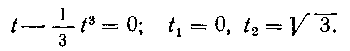
;___L/3 = 0; ti = Qi t2 = VT.
3
Так как данная кривая расположена симметрично относительно оси Ox1 что видно из уравнений кривой, то
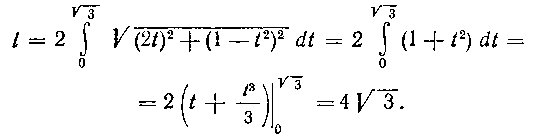
VT VH
I = 2 j V(It)2 - j— (I — t2)2 dt = 2 j (I - f t2) dt =
о о
VH
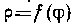
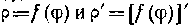
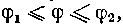
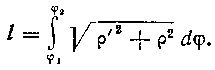
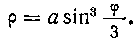
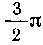
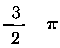
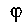
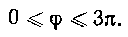
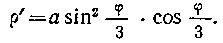
0 < ф < Зя. Найдем р'=а sin2 — • cos —. Вычислим
3 3
Рекомендуется подробнее исследовать данную функцию и построить ее график.
Из теоретического курса известно, что длина дуги кривой р=/(ф), заданной в полярной системе координат, где функции р=/ (ф) и р' = [/(ф)]' непрерывны на ф2 < ф <ф2, вычисляется по формуле:
1 = J ]/У2 + P2 dtp.
<Р I
496. Найти длину кривой: р = a sin3 —.
3
Решение. Найдем пределы интегрирования. Когда п 3
угол ф изменяется от 0 до —я, полярный радиус р воз-
растает от 0 до а. Затем при изменении угла ф от — 7г
до Зл величина р убывает от а до 0. Таким образом, 0 < ф <
сумму:
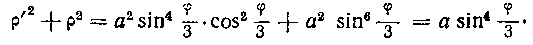
Длина дуги данной кривой равна:
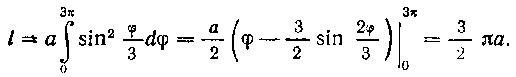
497. Вычислить длину кардиоиды: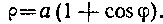
Решение. Так как данная функция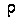
—четная, то, следовательно, кривая расположена симметрично относительно Полярной оси. Поэтому достаточно найти половину длины д<уги кардиоиды, для которой полярный угол ф изменяется от 0 до я, и удвоить полученный результат:
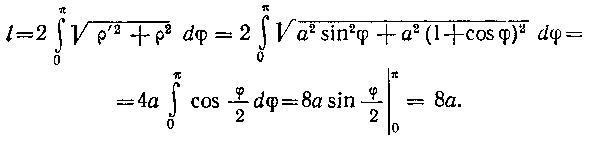
498. Вычислить длину дуги астроиды:
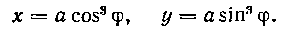
499. Вычислить длину дуги эволюты круга: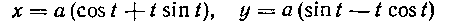 
от
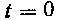До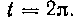
500. Вычислить длину одного витка спирали Архимеда:
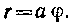
501. Вычислить длину окружности: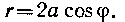
502. Найти длину дуги гиперболической спирали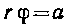
от точки
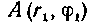До точки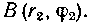
| < Предыдущая | Следующая > |
|---|
