Вариант № 22
1. Исследовать числовой ряд на сходимость: ![]() .
.
Применим признак сравнения в предельной форме. Будем сравнивать данный ряд со сходящимся рядом ![]() :
: 
 . Ряд
. Ряд ![]() сходится, так как ряд с общим членом
сходится, так как ряд с общим членом ![]() сходится при
сходится при ![]() и расходится при
и расходится при ![]() . В данном случае
. В данном случае ![]() . Следовательно, сходится и ряд
. Следовательно, сходится и ряд ![]() . Ответ: Ряд сходится.
. Ответ: Ряд сходится.
2. Исследовать числовой ряд на сходимость: ![]() .
.
Применим признак д, Аламбера:
 ,так как степень в знаменателе выше степени в числителе. Следовательно, данный ряд сходится. Ответ: Ряд сходится.
,так как степень в знаменателе выше степени в числителе. Следовательно, данный ряд сходится. Ответ: Ряд сходится.
3. Исследовать числовой ряд на сходимость: ![]() .
.
Имеем ![]() . Функция
. Функция ![]() удовлетворяет условиям интегрального признака Коши. Действительно,
удовлетворяет условиям интегрального признака Коши. Действительно, ![]() монотонно убывает на
монотонно убывает на ![]() и, следовательно, интеграл
и, следовательно, интеграл  и исходный ряд сходятся или расходятся одновременно. Имеем
и исходный ряд сходятся или расходятся одновременно. Имеем 
![]() . Интеграл сходится, следовательно, сходится и данный ряд. Ответ: Ряд сходится.
. Интеграл сходится, следовательно, сходится и данный ряд. Ответ: Ряд сходится.
4. Исследовать ряд на абсолютную или условную сходимость: ![]() .
.
Рассмотрим ряд  . Применим признак д, Аламбера:
. Применим признак д, Аламбера:
 . Следовательно, рассматриваемый ряд сходится абсолютно. Ответ: Ряд сходится абсолютно.
. Следовательно, рассматриваемый ряд сходится абсолютно. Ответ: Ряд сходится абсолютно.
5. Определить область сходимости функционального ряда: ![]() .
.
Применим признак д, Аламбера к ряду  :
:  . Ряд сходится, если этот предел будет меньше единицы:
. Ряд сходится, если этот предел будет меньше единицы: ![]() , т. е.
, т. е. ![]() . Или
. Или ![]() . Следовательно, интервал
. Следовательно, интервал ![]() является интервалом сходимости данного ряда. Исследуем ряд на концах интервала. При
является интервалом сходимости данного ряда. Исследуем ряд на концах интервала. При ![]() получим знакочередующийся числовой ряд
получим знакочередующийся числовой ряд ![]() , который сходится по признаку Лейбница. При
, который сходится по признаку Лейбница. При ![]() получим числовой ряд
получим числовой ряд ![]() , который сходится по признаку сравнения со сходящимся рядом
, который сходится по признаку сравнения со сходящимся рядом ![]() (степень знаменателя больше единицы). Действительно,
(степень знаменателя больше единицы). Действительно, ![]() . Ответ: Областью сходимости ряда является множество
. Ответ: Областью сходимости ряда является множество ![]()
6. Определить область сходимости функционального ряда: ![]() .
.
Применим признак д, Аламбера к ряду  :
:  . Ряд сходится, если этот предел будет меньше единицы:
. Ряд сходится, если этот предел будет меньше единицы: ![]() , т. е.
, т. е. ![]() или
или ![]() . Следовательно, ряд сходится при
. Следовательно, ряд сходится при ![]() и
и ![]() . Исследуем ряд на концах интервала. При
. Исследуем ряд на концах интервала. При ![]() получим числовой ряд
получим числовой ряд ![]() , который сходится по признаку Лейбница, при
, который сходится по признаку Лейбница, при ![]() получим числовой ряд
получим числовой ряд ![]() , который сходится как ряд типа
, который сходится как ряд типа ![]() , где
, где ![]() . Ответ: Областью сходимости ряда является множество
. Ответ: Областью сходимости ряда является множество ![]()
7. Определить область сходимости функционального ряда: ![]() .
.
Заметим, что область определения членов ряда является множество ![]() . Применим признак д, Аламбера к ряду
. Применим признак д, Аламбера к ряду  :
: 
 . Ряд сходится, если этот предел будет меньше единицы:
. Ряд сходится, если этот предел будет меньше единицы: ![]() , т. е.
, т. е. ![]() или
или ![]() . Из первого неравенства получим
. Из первого неравенства получим ![]() , из второго -
, из второго - ![]() . Сопоставляя с областью определениия ряда, находим, что ряд сходится при
. Сопоставляя с областью определениия ряда, находим, что ряд сходится при ![]() . Исследуем ряд на концах интервала. При
. Исследуем ряд на концах интервала. При ![]() получим числовой ряд
получим числовой ряд ![]() , а при
, а при ![]() - ряд
- ряд ![]() . Оба ряда расходятся, так как не выполняется необходимый признак сходимости. Ответ: Областью сходимости ряда является множество
. Оба ряда расходятся, так как не выполняется необходимый признак сходимости. Ответ: Областью сходимости ряда является множество ![]() .
.
8. Разложить указанную функцию в ряд Тейлора по степеням ![]() . Указать область сходимости:
. Указать область сходимости: ![]() .
.
Воспользуемся известным разложением функции ![]() :
:
![]() . Этот ряд сходится при
. Этот ряд сходится при ![]() . Преобразуем исходную функцию:
. Преобразуем исходную функцию: ![]() . В записанном выше разложении логарифмической функции положим
. В записанном выше разложении логарифмической функции положим ![]() , получим:
, получим: ![]() Или
Или ![]() . Ряд сходится при
. Ряд сходится при ![]() или
или ![]() .
.
Ответ: ![]() .
.
9. Указанную функцию разложить в ряд Маклорена, используя разложения в ряд функций ![]() указать область сходимости:
указать область сходимости:  .
.
Воспользуемся разложением функции ![]() в ряд Маклорена:
в ряд Маклорена: ![]() . Этот ряд сходится при
. Этот ряд сходится при ![]() . Подставим в этот ряд
. Подставим в этот ряд ![]() Тогда
Тогда ![]() и
и ![]()
![]() . Областью сходимости ряда будет
. Областью сходимости ряда будет ![]() . Ответ:
. Ответ:  ,
, ![]() .
.
10. Вычислить приближённо с точностью до 10-4:  .
.
Воспользуемся формулой ![]() . Получим
. Получим ![]() . Тогда
. Тогда 

![]() . В соответствии с теоремой Лейбница заданная точность будет достигнута, если первое отбрасываемое слагаемое будет по абсолютной величине меньше, чем
. В соответствии с теоремой Лейбница заданная точность будет достигнута, если первое отбрасываемое слагаемое будет по абсолютной величине меньше, чем ![]() . В данном случае
. В данном случае ![]() . Очевидно, что
. Очевидно, что ![]() . Следовательно, достаточно взять четыре первых слагаемых:
. Следовательно, достаточно взять четыре первых слагаемых:  . Ответ:
. Ответ: 
11. Вычислить предел, используя разложение функций в ряд Тейлора: ![]() .
.
Преобразуем предел ![]()
![]() . Так как
. Так как ![]()
![]() , то
, то ![]()
![]() .
.
Ответ: ![]() .
.
12. Найти сумму ряда:![]() .
.
Обозначим сумму ряда через S(X). Тогда ![]()
![]() . Но
. Но ![]() есть сумма бесконечно убывающей геометрической прогрессии при
есть сумма бесконечно убывающей геометрической прогрессии при ![]() . Следовательно,
. Следовательно, 

![]() . Ответ:
. Ответ: ![]() .
.
13. Найти сумму ряда:![]() .
.
Обозначим сумму ряда через S(X). Тогда ![]()
 . Но
. Но ![]() есть суммы бесконечно убывающих геометрических прогрессий при
есть суммы бесконечно убывающих геометрических прогрессий при ![]() . Следовательно,
. Следовательно, 

![]() .
.
Ответ: ![]() .
.
14. Получить решение дифференциального уравнения 1-го и 2-го порядков в виде степенного ряда или ряда Тейлора: ![]()
Будем искать решение уравнения в виде ![]() , где
, где ![]() . Будем последовательно вычислять производные
. Будем последовательно вычислять производные ![]() :
: ![]() ,
, ![]()
![]()
![]()
![]() . Следовательно,
. Следовательно, ![]()
![]() . Тогда
. Тогда ![]() .
.
Ответ: ![]() .
.
15. Получить решение дифференциального уравнения 1-го и 2-го порядков в виде степенного ряда или ряда Тейлора: ![]()
Ищем решение уравнения в виде ![]() . Тогда
. Тогда ![]() . Подставляя это в исходное уравнение, получим:
. Подставляя это в исходное уравнение, получим: ![]() . Первую сумму можно записать в следующем виде:
. Первую сумму можно записать в следующем виде: ![]() , вторую сумму – в виде
, вторую сумму – в виде ![]() . Тогда
. Тогда ![]() . Объединим все суммы, выделяя «лишнее» слагаемое:
. Объединим все суммы, выделяя «лишнее» слагаемое: ![]() . Это равнество должно выполняться для различных значений X. Это возможно лишь тогда, когда коэффициенты при всех степенях X будут равны нулю, т. е.
. Это равнество должно выполняться для различных значений X. Это возможно лишь тогда, когда коэффициенты при всех степенях X будут равны нулю, т. е. ![]() и
и ![]() . Отсюда получаем рекуррентную формулу:
. Отсюда получаем рекуррентную формулу: ![]() Следовательно,
Следовательно, ![]() . Воспользуемся начальными условиями:
. Воспользуемся начальными условиями: ![]() . Получим:
. Получим: ![]() . Таким образом,
. Таким образом, ![]() .
.
Ответ: ![]() .
.
16. Разложить заданную графиком периодическую функцию в ряд Фурье:
 По графику определяем
По графику определяем ![]() .
.
Разложение функции в ряд Фурье имеет вид: ![]() . Вычислим коэффициенты
. Вычислим коэффициенты ![]() :
: 
 . Вычислим коэффициенты
. Вычислим коэффициенты ![]() :
: 
 . Таким образом,
. Таким образом, ![]() .
.
Ответ: ![]() .
.
17. Разложить функцию в ряд Фурье на ![]() :
: ![]()
Вычисляем коэффициенты разложения ![]() данной функции в ряд Фурье. Так как функция чётная, то все
данной функции в ряд Фурье. Так как функция чётная, то все ![]() . Вычислим
. Вычислим ![]() .
.  . Из таблиц находим (при
. Из таблиц находим (при ![]() ):
):  . Следовательно,
. Следовательно, ![]() если
если ![]() чётное и
чётное и ![]() , если
, если ![]() нечётное. Положим
нечётное. Положим ![]() . Тогда нечётным значениям
. Тогда нечётным значениям ![]() соответствуют числа
соответствуют числа ![]() . Таким образом,
. Таким образом, ![]() . Ответ:
. Ответ: ![]() .
.
18. Найти разложение функции ряд Фурье в комплексной форме на ![]() :
: ![]() .
.
В комплексной форме ряд Фурье функции ![]() периода
периода ![]() имеет вид:
имеет вид: 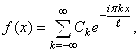 где
где 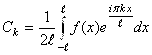 . В данном случае
. В данном случае 


 . Таким образом,
. Таким образом,  . Ответ:
. Ответ:  .
.
19. Функцию ![]() представить интегралом Фурье в действительной форме:
представить интегралом Фурье в действительной форме:
 .
.
Представление функции интегралом Фурье в действительной форме имеет вид 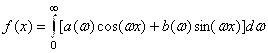 , где
, где 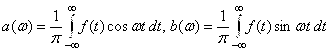 . Заданная функция является нечётной и, следовательно,
. Заданная функция является нечётной и, следовательно, 

![]() . Таким образом,
. Таким образом,  .
.
Ответ: 
20. Функцию ![]() представить интегралом Фурье в комплексной форме:
представить интегралом Фурье в комплексной форме:
 .
.
Представление функции интегралом Фурье в комплексной форме имеет вид 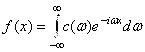 , где
, где 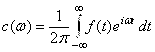 . Вычислим
. Вычислим ![]() :
: 


![]() . Таким образом,
. Таким образом,  .
.
Ответ: 
| < Предыдущая | Следующая > |
|---|