Вариант № 02
В задачах 1-9 найти общие решения уравнений и частные решения, если есть начальные условия.
1. ![]() . Уравнение является однородным. Сделаем замену
. Уравнение является однородным. Сделаем замену ![]() Тогда
Тогда ![]() . Получим уравнение
. Получим уравнение ![]() , или
, или ![]() . Запишем уравнение в дифференциалах:
. Запишем уравнение в дифференциалах: ![]() . Разделяем переменные:
. Разделяем переменные: ![]() . Интегрируем уравнение:
. Интегрируем уравнение: ![]() . Получим:
. Получим: ![]() . Вернёмся к переменной Y, делая обратную замену U=Y/X:
. Вернёмся к переменной Y, делая обратную замену U=Y/X: ![]() . Определим постоянную С из начальных условий:
. Определим постоянную С из начальных условий: ![]() , отсюда C=−3/2. Подставляя это значение в общее решение, получим частное решение:
, отсюда C=−3/2. Подставляя это значение в общее решение, получим частное решение: ![]() . Ответ:
. Ответ: ![]() .
.
2. ![]() . Уравнение является линейным. Решим его методом Бернулли. Будем искать решение в виде произведения Y=U∙V, где U и V неизвестные функции, определяемые в данном случае уравнениями
. Уравнение является линейным. Решим его методом Бернулли. Будем искать решение в виде произведения Y=U∙V, где U и V неизвестные функции, определяемые в данном случае уравнениями ![]() и
и ![]() . Решим первое уравнение:
. Решим первое уравнение: ![]() или
или ![]() . Отсюда
. Отсюда ![]() (произвольная постоянная добавляется при решении второго уравнения). Потенцируя, находим:
(произвольная постоянная добавляется при решении второго уравнения). Потенцируя, находим: ![]() . Подставим найденную функцию U во второе уравнение и решим его:
. Подставим найденную функцию U во второе уравнение и решим его: ![]() или
или
 . Таким образом, общее решение имеет вид:
. Таким образом, общее решение имеет вид: ![]() . Найдём C, исходя из начальных условий:
. Найдём C, исходя из начальных условий: ![]() . Таким образом, частное решение есть
. Таким образом, частное решение есть ![]() . Ответ:
. Ответ: ![]() .
.
3. ![]() . Это уравнение Бернулли. Его можно решать непосредственно как линейное уравнение, применяя метод вариации произвольной постоянной. Решим однородное уравнение:
. Это уравнение Бернулли. Его можно решать непосредственно как линейное уравнение, применяя метод вариации произвольной постоянной. Решим однородное уравнение: ![]() или
или ![]() . Потенцируя, находим:
. Потенцируя, находим: ![]() . Будем предполагать, что решение исходного уравнения имеет
. Будем предполагать, что решение исходного уравнения имеет
такую же структуру, но C=C(X), т. е. ![]() , где C(X) – некоторая неизвестная функция. Определим эту функцию, подставляя данное (предполагаемое) решение в исходное уравнение. Найдём
, где C(X) – некоторая неизвестная функция. Определим эту функцию, подставляя данное (предполагаемое) решение в исходное уравнение. Найдём ![]() . Тогда
. Тогда ![]() . Или
. Или ![]() . Разделяем переменные:
. Разделяем переменные: ![]() . Интегрируем уравнение:
. Интегрируем уравнение:  . Следовательно,
. Следовательно, ![]() или
или ![]() . Общие решение уравнения
. Общие решение уравнения ![]() . Воспользуемся начальными условиями:
. Воспользуемся начальными условиями: ![]() , т. е. C1=−2. Тогда частным решением будет
, т. е. C1=−2. Тогда частным решением будет ![]() . Ответ:
. Ответ: ![]() .
.
4. ![]() Уравнение является уравнением в полных дифференциалах. Действительно,
Уравнение является уравнением в полных дифференциалах. Действительно, ![]()
![]() . Левая часть этого уравнения представляет полный дифференциал некоторой функции U(X,Y), так что
. Левая часть этого уравнения представляет полный дифференциал некоторой функции U(X,Y), так что ![]() и
и ![]() . Проинтегрируем второе уравнение по Y:
. Проинтегрируем второе уравнение по Y:
![]() , где φ(X) – произвольная функция. Найдём эту функцию, пользуясь первым уравнением. С одной стороны
, где φ(X) – произвольная функция. Найдём эту функцию, пользуясь первым уравнением. С одной стороны ![]() . С другой стороны,
. С другой стороны, ![]() . Приравнивая эти выражения, получим:
. Приравнивая эти выражения, получим: ![]() . Отсюда,
. Отсюда, ![]() . Следовательно,
. Следовательно, ![]() Согласно уравнению, DU=0. Решением уравнения будет U(x, y)=C. В данном случае
Согласно уравнению, DU=0. Решением уравнения будет U(x, y)=C. В данном случае ![]()
Ответ: ![]()
5. ![]() Уравнение второго порядка, допускающее понижение порядка. В уравнении отсутствует независимая переменная X. Сделаем замену
Уравнение второго порядка, допускающее понижение порядка. В уравнении отсутствует независимая переменная X. Сделаем замену ![]() . Тогда
. Тогда ![]() . Получим однородное уравнение первого порядка:
. Получим однородное уравнение первого порядка: ![]() Сделаем подстановку:
Сделаем подстановку: ![]() . Тогда
. Тогда ![]() Отсюда следует, что
Отсюда следует, что ![]() является частным решением исходного уравнения. Исключаем его из дальнейшего рассмотрения:
является частным решением исходного уравнения. Исключаем его из дальнейшего рассмотрения: ![]() Или
Или ![]() Интегрируем:
Интегрируем: ![]() или
или ![]() . Вернёмся к переменной P:
. Вернёмся к переменной P: ![]() . Из начальных условий следует, что
. Из начальных условий следует, что ![]() и
и ![]() при
при ![]() . Подставляя это в полученное равенство, находим
. Подставляя это в полученное равенство, находим ![]() . Тогда
. Тогда ![]() или
или ![]() . Решение
. Решение ![]() не удовлетворяет начальным условиям. Таким образом,
не удовлетворяет начальным условиям. Таким образом, ![]() . Подставляя сюда начальные условия, находим
. Подставляя сюда начальные условия, находим ![]() . Окончательно,
. Окончательно, ![]() . Ответ:
. Ответ: ![]() .
.
6. ![]() Линейное неоднородное уравнение второго порядка. Решим уравнение методом вариации произвольных постоянных. Найдём сначала решение однородного уравнения
Линейное неоднородное уравнение второго порядка. Решим уравнение методом вариации произвольных постоянных. Найдём сначала решение однородного уравнения ![]() Характеристическое уравнение
Характеристическое уравнение ![]() имеет два корня:
имеет два корня: ![]() . Получаем два частных решений:
. Получаем два частных решений: ![]() . Общее решение однородного уравнения имеет вид:
. Общее решение однородного уравнения имеет вид: ![]() . Будем считать, что решение неоднородного уравнения имеет такую же структуру, но С1 и С2 являются функциями переменной Х:
. Будем считать, что решение неоднородного уравнения имеет такую же структуру, но С1 и С2 являются функциями переменной Х: ![]() . Тогда, в соответствии с методом вариации произвольных постоянных, неизвестные функции С1(Х) и С2(Х) определяются системой уравнений:
. Тогда, в соответствии с методом вариации произвольных постоянных, неизвестные функции С1(Х) и С2(Х) определяются системой уравнений:
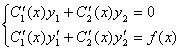 , где F(X) – правая часть неоднородного уравнения. В данном случае имеем систему:
, где F(X) – правая часть неоднородного уравнения. В данном случае имеем систему:  . Оба уравнения сократим на
. Оба уравнения сократим на ![]() :
:  . Из первого уравнения
. Из первого уравнения ![]() . Подставим это во второе уравнение:
. Подставим это во второе уравнение: ![]() или
или ![]() . Отсюда
. Отсюда ![]() , т. е.
, т. е. ![]() или
или ![]() . Далее,
. Далее, ![]() . Интегрируя, получаем:
. Интегрируя, получаем: ![]() . Следовательно, решением неоднородного уравнения будет
. Следовательно, решением неоднородного уравнения будет ![]() . Теперь можно вернуться к прежним обозначениям произвольных постоянных. Положим С4=С1 и С3 =С2. Окончательно,
. Теперь можно вернуться к прежним обозначениям произвольных постоянных. Положим С4=С1 и С3 =С2. Окончательно, ![]() . Ответ:
. Ответ: ![]() .
.
7. ![]() . Линейное неоднородное уравнение второго порядка. Найдём сначала решение однородного уравнения
. Линейное неоднородное уравнение второго порядка. Найдём сначала решение однородного уравнения ![]() Характеристическое уравнение
Характеристическое уравнение ![]() имеет два корня:
имеет два корня: ![]() . Получаем два частных решения:
. Получаем два частных решения: ![]() . Общее решение однородного уравнения имеет вид:
. Общее решение однородного уравнения имеет вид: ![]() . Найдём частное
. Найдём частное
решение неоднородного уравнения, исходя из структуры его правой части: ![]() . Найдём производные YЧн::
. Найдём производные YЧн:: ![]()
![]() . Подставим это в исходное уравнение:
. Подставим это в исходное уравнение:
![]() . Отсюда находим
. Отсюда находим ![]() . Или
. Или ![]() . Следовательно,
. Следовательно, ![]() . Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного:
. Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного: ![]() . Ответ:
. Ответ: ![]() .
.
8. ![]() . Линейное неоднородное уравнение второго порядка. Найдём сначала решение однородного уравнения
. Линейное неоднородное уравнение второго порядка. Найдём сначала решение однородного уравнения ![]() Характеристическое уравнение
Характеристическое уравнение ![]() имеет два корня:
имеет два корня: ![]() . Получаем два частных решения:
. Получаем два частных решения: ![]() . Общее решение однородного уравнения имеет вид:
. Общее решение однородного уравнения имеет вид: ![]() . Найдём частное решение неоднородного уравнения, исходя из структуры его правой части:
. Найдём частное решение неоднородного уравнения, исходя из структуры его правой части: ![]() . Здесь множитель Х обусловлен тем, что корень характеристического уравнения R1=−1 имеет кратность 1. Значение этого корня совпадает с коэффициентом α в экспоненте EαX, «стоящей» в правой части уравнения (α=−1). Найдём производные YЧн::
. Здесь множитель Х обусловлен тем, что корень характеристического уравнения R1=−1 имеет кратность 1. Значение этого корня совпадает с коэффициентом α в экспоненте EαX, «стоящей» в правой части уравнения (α=−1). Найдём производные YЧн:: ![]()
![]()
![]() . Подставим это в исходное уравнение:
. Подставим это в исходное уравнение:
![]() . Отсюда находим
. Отсюда находим ![]() . Или
. Или ![]() . Следовательно,
. Следовательно, ![]() . Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного:
. Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного: ![]() . Воспользуемся начальными условиями:
. Воспользуемся начальными условиями: ![]() . По первому условию
. По первому условию ![]() . Найдём
. Найдём ![]() . Тогда, по второму условию,
. Тогда, по второму условию, ![]() . Решая систему
. Решая систему  , находим:
, находим: ![]() . Частное решение уравнения будет
. Частное решение уравнения будет ![]() . Или
. Или ![]() .
.
Ответ: ![]() .
.
9. ![]() . Линейное неоднородное уравнение второго порядка. Найдём сначала решение однородного уравнения
. Линейное неоднородное уравнение второго порядка. Найдём сначала решение однородного уравнения ![]() Характеристическое уравнение
Характеристическое уравнение ![]() имеет один корень кратности 2:
имеет один корень кратности 2: ![]() . Получаем два частных решения:
. Получаем два частных решения: ![]() . Общее решение однородного уравнения имеет вид:
. Общее решение однородного уравнения имеет вид: ![]() . Найдём частное решение неоднородного уравнения, исходя из структуры его правой части:
. Найдём частное решение неоднородного уравнения, исходя из структуры его правой части: ![]() . Найдём производные YЧн::
. Найдём производные YЧн::
![]()
![]()
![]() . Подставим это в исходное уравнение:
. Подставим это в исходное уравнение:
![]()
![]() . Сокращая на
. Сокращая на ![]() и приравнивая коэффициенты при одинаковых функциях в левой и правой частях равенства, получим: Отсюда находим
и приравнивая коэффициенты при одинаковых функциях в левой и правой частях равенства, получим: Отсюда находим ![]() . Или
. Или![]() . Следовательно,
. Следовательно, ![]() . Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного:
. Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного: ![]() .
.
Ответ: ![]() .
.
10. Решить систему линейных однородных дифференциальных уравнений первого порядка с постоянными коэффициентами ![]() , где
, где 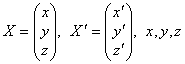 - функции от T, M – матрица коэффициентов, при начальных условиях
- функции от T, M – матрица коэффициентов, при начальных условиях ![]() :
:
 .
.
Запишем систему по исходным данным:
 . Ищем решение в виде
. Ищем решение в виде 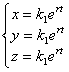 . Тогда
. Тогда 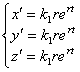 . Подставляя это в систему, получим систему алгебраических уравнений, которая определяет неизвестные коэффициенты
. Подставляя это в систему, получим систему алгебраических уравнений, которая определяет неизвестные коэффициенты ![]() :
:  . Приравнивая определитель системы к нулю, получим характеристическое уравнение исходной системы:
. Приравнивая определитель системы к нулю, получим характеристическое уравнение исходной системы:  . Раскроим определитель:
. Раскроим определитель: ![]() . Или
. Или ![]() . Следовательно,
. Следовательно, ![]() . При
. При ![]() получим систему:
получим систему:  . Отбросим первое уравнение, как линейно зависимое. Получим
. Отбросим первое уравнение, как линейно зависимое. Получим ![]() . Положим
. Положим ![]() . Тогда
. Тогда ![]() . Получили первое частное решение:
. Получили первое частное решение: ![]() . При
. При ![]() получим систему:
получим систему:  . Отбросим первое уравнение, как линейно зависимое. Получим
. Отбросим первое уравнение, как линейно зависимое. Получим ![]() . Положим
. Положим ![]() . Тогда
. Тогда ![]() . Получили второе частное решение:
. Получили второе частное решение: ![]() .
.
При ![]() получим систему:
получим систему:  . Отбросим второе уравнение, как линейно зависимое. Получим
. Отбросим второе уравнение, как линейно зависимое. Получим ![]() . Положим
. Положим ![]() . Тогда
. Тогда ![]() . Получили третье частное решение:
. Получили третье частное решение: ![]() . Общее решение записывается как линейная комбинация частных решений:
. Общее решение записывается как линейная комбинация частных решений:  .
.
Найдём произвольные постоянные, пользуясь начальными условиями. При T=0 получим систему:  . Складывая первое уравнение со вторым и первое уравнение с третьим, получим:
. Складывая первое уравнение со вторым и первое уравнение с третьим, получим:  . Следовательно,
. Следовательно, ![]() . Таким образом, частное решение системы следующее:
. Таким образом, частное решение системы следующее:  .
.
Ответ:  .
.
11. Найдите уравнение кривой, проходящей через точку M(1; 2) и обладающей свойством, что отрезок любой её касательной, заключённой между осями координат, делится в точке касания в отношении 2:3, считая от оси ординат.
Уравнение касательной к кривой ![]() в точке
в точке ![]() имеет вид
имеет вид ![]() . Найдём точки пересечения касательной с осями координат. Положим Y=0. Тогда
. Найдём точки пересечения касательной с осями координат. Положим Y=0. Тогда ![]() или
или ![]() . Точка М1
. Точка М1![]() является точкой пересечения оси ОХ. Положим X=0. Тогда
является точкой пересечения оси ОХ. Положим X=0. Тогда ![]() или
или ![]() . Точка М2
. Точка М2![]() является точкой пересечения оси ОУ. По условию задачи
является точкой пересечения оси ОУ. По условию задачи  , т. е.
, т. е.  . Или
. Или  . Это равенство справедливо для любой точки
. Это равенство справедливо для любой точки ![]() . Заменим эту точку произвольной точкой
. Заменим эту точку произвольной точкой ![]() , лежащей на кривой
, лежащей на кривой ![]() . Получим:
. Получим: ![]() , или
, или ![]() , или
, или ![]() . Разрешим уравнение относительно
. Разрешим уравнение относительно ![]() :
: ![]()
![]() . Получаем два уравнения:
. Получаем два уравнения: ![]() и
и ![]() . Второе уравнение не имеет действительных решений. Рассмотрим первое:
. Второе уравнение не имеет действительных решений. Рассмотрим первое: ![]() . Разделяем переменные:
. Разделяем переменные: ![]() . Интегрируем:
. Интегрируем: ![]() или
или ![]() . Найдём C, учитывая, что кривая проходит через точку М(1, 2):
. Найдём C, учитывая, что кривая проходит через точку М(1, 2): ![]() . Таким образом,
. Таким образом, ![]() или
или ![]() . Кривые
. Кривые ![]() и
и ![]() удовлетворяют условию задачи. Первая кривая соответствует внешнему делению отрезка, а вторая – внутреннему делению. Повидимому в задаче предполагается внутреннее деление. Ответ:
удовлетворяют условию задачи. Первая кривая соответствует внешнему делению отрезка, а вторая – внутреннему делению. Повидимому в задаче предполагается внутреннее деление. Ответ: ![]() .
.
12. По закону Торричелли скорость истечения жидкости равна ![]() , где X – высота уровня жидкости над отверстием. Определить время полного истечения воды из цилиндрического бака высотой H=6м, диаметром 2L=4м с горизонтальной через круглое отверстие в нижней части бака диаметром 2R=1/6м.
, где X – высота уровня жидкости над отверстием. Определить время полного истечения воды из цилиндрического бака высотой H=6м, диаметром 2L=4м с горизонтальной через круглое отверстие в нижней части бака диаметром 2R=1/6м.
Обозначим через Y(T) объём жидкости в баке в момент времени T. Очевидно, что ![]() , где X=X(T) – высота уровня жидкости в баке в момент времени T. Тогда
, где X=X(T) – высота уровня жидкости в баке в момент времени T. Тогда ![]() . Сечение круглого отверстия в дне равно
. Сечение круглого отверстия в дне равно ![]() . Следовательно, скорость уменьшения объёма жидкости будет равна
. Следовательно, скорость уменьшения объёма жидкости будет равна ![]() . Таким образом,
. Таким образом, ![]() , или
, или ![]() . Найдём
. Найдём ![]() :
: ![]() . С другой стороны
. С другой стороны  (см. рисунок – сечение бака). Тогда
(см. рисунок – сечение бака). Тогда ![]() (по правилу
(по правилу ![]() Дифференцирования интеграла). Подставляя это в предыдущее
Дифференцирования интеграла). Подставляя это в предыдущее ![]() Уравнение, получим:
Уравнение, получим:  . Разделяем переменные:
. Разделяем переменные:  . Интегрируем уравнение:
. Интегрируем уравнение:  . Рассмотрим левый интеграл:
. Рассмотрим левый интеграл: 


 . Таким образом,
. Таким образом,  . Подставляя сюда начальное условие
. Подставляя сюда начальное условие ![]() , получим:
, получим: ![]() ,
,  . По истечению всей жидкости получим
. По истечению всей жидкости получим ![]() . Следовательно,
. Следовательно,  . Подставляя сюда все числовые данные и делая вычисления, получим:
. Подставляя сюда все числовые данные и делая вычисления, получим: ![]() мин (секунды были переведены в минуты).
мин (секунды были переведены в минуты).
Ответ: ![]() Мин.
Мин.
| < Предыдущая | Следующая > |
|---|