Теория вероятности 04
Задание №1. Монету бросают дважды. Какова вероятность выпадения герба только один раз?
Обозначим события:
При первом броске выпал герб;
При втором броске выпал герб;
При первом броске не выпал герб;
При втором броске не выпал герб.
Вероятности этих событий (по классическому определению вероятностей) равны: 
Тогда 
Основное событие А — выпадение герба только один раз.
По формулам сложения и умножения вероятностей
Ответ: 
Задание №2. На складе хранятся 30 изделий завода 1, 15 изделий – завода 2, 20 изделий завода 3. Вероятность получения бездефектного изделия на первом заводе – 0.9, на втором – 0.8, на третьем – 0.7.
А) Найти вероятность того, что извлеченное наудачу изделие будет бездефектным.
Б) Извлеченное наудачу изделие оказалось бездефектным. Какова вероятность, что оно изготовлено на заводе 3?
Основное событие А 
извлеченное наудачу изделие будет бездефектным.
Гипотезы:
Выбранное изделие поступило с первого завода;
Выбранное изделие поступило со второго завода;
Выбранное изделие поступило с третьего завода.
Вероятности гипотез (по классическому определению вероятности):
Условные вероятности:
А) Вероятность события А по формуле полной вероятности равна:
Б) Вероятность того, что изделие изготовлено на заводе 3 по формуле Байеса:
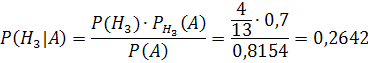
Ответ: 
Задание №3. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка 
= 0.9, для второго 
= 0.8. Найти вероятность того, что при 6 выстрелах стрелки одновременно попадут в мишень:
А) менее трех раз; б) не менее трех раз; с) хотя бы один раз; д) найти наивероятнейшее число парных попаданий при 6 выстрелах.
Решение
Обозначим события:
Первый стрелок поразил цель;
Второй стрелок поразил цель;
По условию вероятности этих событий равны (по условию):
Вероятность 
одновременного попадания при одном парном выстреле равна:
Воспользуемся формулой Бернулли. Если производится 
независимых испытаний, при каждом из которых вероятность осуществления события 
постоянна и равна 
, а вероятность противоположного события равна 
, то вероятность того, что при этом событие осуществляется ровно 
раз, вычисляется по формуле
Где 
— число сочетаний из элементов по .
А) Для данного случая
Вероятность события A – при 6 выстрелах стрелки одновременно попадут в мишень менее трех раз, равна:
б) Для данного случая
Вероятность события B – при 6 выстрелах стрелки одновременно попадут в мишень не менее трех раз, равна:
c) Для данного случая
Вероятность события C – при 6 выстрелах стрелки одновременно попадут в мишень хотя бы один раз, равна:
Д) найдем наивероятнейшее число парных попаданий при 6 выстрелах.
Если производится независимых испытаний, при каждом из которых вероятность осуществления события постоянна и равна , а вероятность противоположного события равна , то число успехов 
, при котором достигается наибольшая из возможных вероятностей, определяется как целое число на промежутке по формуле:
Для данного случая:
Исходя из того, что целое число, наивероятнейшее число равно 5.
Ответ: 
Задание №4. При обследовании уставных фондов банков установлено, что 6-я часть банков имеют уставной фонд свыше 100 млн. руб. Найти вероятность того, что среди 500 банков имеют уставной фонд свыше 100 млн. руб.: a) не менее 100; b) от 100 до 200 включительно.
Решение
Интегральная теорема Лапласа. Если вероятность наступления события в каждом из независимых испытаний постоянна и отлична от нуля и единицы, то вероятность того, что в независимых испытаниях событие наступит не менее чем 
раз и не более чем 
раза, определяется по формуле:
Где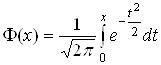 
, 
, 
.
А) В данном случае 
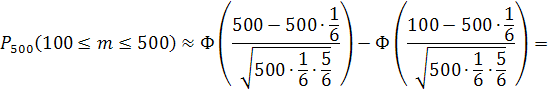
Б) В данном случае
Ответ: 
Задание №5. В ящике содержится 11 деталей, среди которых 4 бракованных. Сборщик наудачу извлекает 3 деталей.
1. Найти вероятность того, что среди извлеченных деталей: a) 3 бракованных; b) одна бракованная; c) две бракованные; d) хотя бы одна бракованная.
2. Составить закон распределения случайной величины X – числа бракованных деталей среди извлеченных.
3. Найти M(X), D(X), 
.
4. Вычислить P(1<X<4)
Решение
1. По классическому определению вероятности:
a) среди извлеченных деталей 3 бракованных.
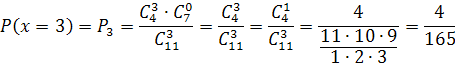
B) среди извлеченных деталей одна бракованная.
C) среди извлеченных деталей две бракованные.
D) среди извлеченных деталей хотя бы одна бракованная.
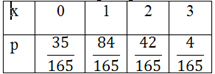
2. Составим закон распределения случайной величины X– числа бракованных деталей среди извлеченных.
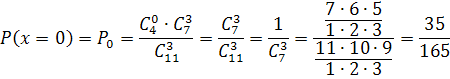
Закон распределения имеет вид:
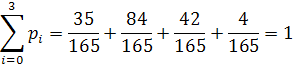
Функция распределения выглядит следующим образом
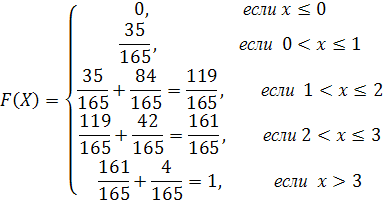
3. Математическое ожидание 
равно:
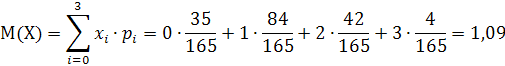
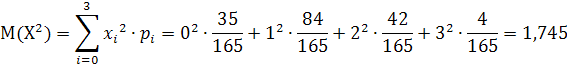
Дисперсия 
равна:
Среднее квадратическое отклонение 
равно
4. Вероятность попадания случайной величины в интервал 
:
Задание №6. Непрерывная случайная величина X задана функцией распределения F(x). Найти плотность распределения F(x), математическое ожидание и дисперсию случайной величины. Изобразить графики функции распределения F(x) и плотности распределения F(x). Найти вероятность попадания случайной величины в интервал 
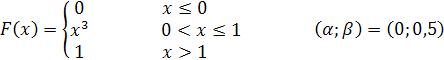
Решение
Плотность распределения вероятности найдем по формуле
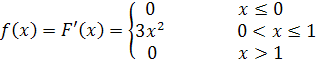
Математическое ожидание случайной величины Х Равно:
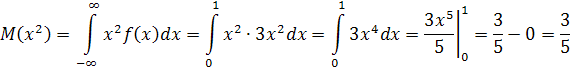
Дисперсия:
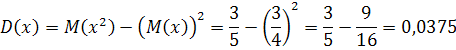
Изобразим графики функции распределения F(x) и плотности распределения F(x).
Вероятность попадания случайной величины Х в интервал 
равна приращению функции распределения на этом интервале:
Задание №7. Известны математическое ожидание 
и среднее квадратичное отклонение 
Нормально распределенной случайной величины X. Найти: A) вероятность попадания этой величины в заданный интервал 
; B) вероятность того, что абсолютная величина X-a отклонения окажется меньше 
C) Вычислить M(3X-2), D(3X-2).
Решение
A) Для нормального закона распределения случайной величины вероятность попадания в заданный интервал равна:
Где 
– функция Лапласа.
При 
B) Вероятность того, что модуль отклонения случайной величины Х от своего математического ожидания 
меньше любого положительного 
, равна
Где – функция Лапласа.
При заданных условиях:
C) вычислим M(3X-2), D(3X-2).
По свойствам математического ожидания:
По свойствам дисперсии:
Задание №8. Заданы среднее квадратичное отклонение σ нормально распределенной случайной величины X, выборочная средняя 
, объем выборки N. Найти доверительные интервалы для оценки неизвестного математического ожидания А с заданной надежностью γ = 0.95.
Решение
Доверительный интервал для математического ожидания A нормально распределенной случайной величины равен:
Где t – такое значение аргумента функции Лапласа, при котором 
.
По таблице функции Лапласа находим t из равенства:
Получаем 
и искомый доверительный интервал имеет вид:
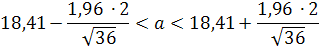
Задание №9. Найти: 1) выборочную дисперсию; 2) выборочное среднее квадратичное отклонение по данному статистическому распределению выборки (в первой строке указаны выборочные варианты XI, а во второй строке – соответствующие частоты NI количественного признака X).
Решение
Общее число значений
1) Найдем выборочное среднее
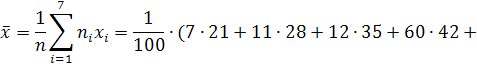
Выборочная дисперсия равна
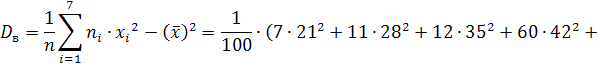
2) Выборочное среднеквадратическое отклонение
Задание №10. Найти выборочное уравнение прямой
Регрессии X на Y по данной корреляционной таблице.
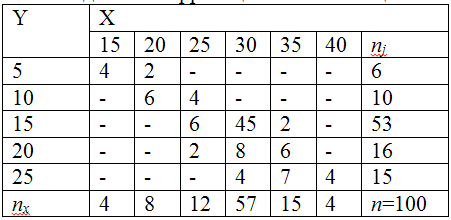
Решение
Найдем необходимые числовые характеристики.
Выборочные средние:
Дисперсии:
Откуда получаем:
И ковариация:
2) Определим коэффициент корреляции
3) Запишем уравнения линий регрессии:
И вычисляя, получаем
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Вентцель Е. С., Овчаров Л. А. Теория вероятностей и ее инженерные приложения. - М.: Наука, 1988. - 416 с.
2. Вентцель Е. С. Теория вероятностей и математическая статистика: – Учебник. - 5-е изд., стереотип. - М.: Высш. шк., 1999. - 576 с.
3. Большев Л. Н., Смирнов Н. В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с.
| < Предыдущая | Следующая > |
|---|
