Теория вероятности 10

Вариант 5

5. Плотность распределения вероятностей непрерывной случайной величины Х имеет вид:

Необходимо:

Определить значение ;

Вычислить математическое ожидание , дисперсию и среднеквадратичное отклонение ;

Найти интегральную функцию распределения вероятностей ;

Построить графики функций ;

Вычислить вероятность выполнения неравенства .

Решение:

Значение определим из условия :

Математическое ожидание , дисперсию и среднеквадратичное отклонение :

Данная функция плотности распределения говорит о том, что Х имеет равномерное распределение на отрезке . Тогда

Интегральная функция распределения:

Строим графики функций:

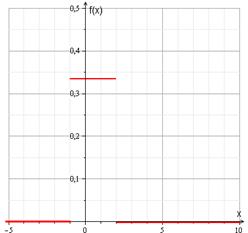
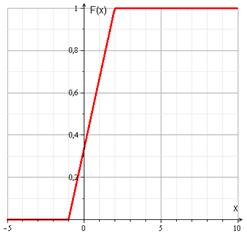
6. Плотность распределения вероятностей непрерывной случайной величины Х имеет вид . Требуется:

Определить значение ;

Вычислить математическое ожидание , дисперсию и среднеквадратичное отклонение ;

Найти интегральную функцию распределения вероятностей ;

Вычислить вероятность выполнения неравенства .

Решение:

Сравнивая заданную плотность распределения

с плотностью нормально распределенной НСВ , находим, что ,

откуда .

Итак, имеем:

Интегральная функция распределения данной НСВ, как величины, распределенной по нормальному закону, принимает вид:

Где – функция Лапласа.

Вероятность того, что значения величины Х принадлежат интервалу (0,5;1,5), вычисляется по формуле

7. В высшем учебном заведении проводилось тестирование студентов с целью выяснения ровня знаний по курсу высшей математики.

Студенты, кроме ответов на предложенные вопросы, должны были указать, сколько времени каждый из них тратил на подготовку

к тесту. Итогом тестирования оказалась генеральная совокупность данных объемом N = 600 с двумя числовыми признаками: результат

тестирования в баллах (признак 1) и время, израсходованное на подготовку к тесту в часах (признак 2).

Нужно:

Создать индивидуальную выборочную совокупность данных (признаки 1 и 2) объемом П = 100 согласно указанному преподавателем

индивидуального номера К І следующего правила: из генеральной совокупности выбрать 100 значений признаков 1 и 2 с последовательными

номерами NN = К, К+5, К+10,...., К+495 (все значения признака 1 увеличить при этом на величину К);

После упорядочения значений признака 1 по возрастанию построить для этого признака интервальный вариационный ряд;

Построить многоугольник и гистограмму выборочного распределения признака 1;

Определить числовые характеристики построенного выборочного распределения: а) выборочную среднюю, б) выборочную дисперсию,

в) выборочное среднеквадратичное отклонение;

Для построенного выборочного распределения проверить гипотезу о том, что признак 1 в генеральной совокупности распределено по

нормальному закону (уровень значимости = 0,05);

При доверительной вероятности = 0,95 определить доверительные интервалы для математического ожидания, дисперсии и

среднеквадратичного отклонения признака 1 в генеральной совокупности, используя для этого первые (20 + Q) Значений признака 1

в начальной (неупорядоченной) выборке; Q - Последняя цифра индивидуального номера К;

Для тех же (20 + Q) Первых значений признаков 1 и 2 построить уравнение прямой линии регрессии Y (признак 1) на X (признак 2) и

уравнение прямой линии регрессии X На У. Определить коэффициенты корреляции и детерминации и объяснить содержание этих коэффициентов.

Построить графики прямых линий регрессии вместе с заданным корреляционным полем

Х	У	Х	У	Х	У	Х	У	Х	У	Х	У
222	34	190	28	336	37	218	38	337	41	227	38
89	17	92	14	205	25	130	24	233	40	254	35
196	33	189	29	66	11	201	11	87	10	330	37
289	39	167	19	172	29	342	37	128	23	192	33
206	30	224	39	337	18	205	25	170	26	277	41
77	20	251	39	228	37	66	11	192	29	187	31
207	25	115	13	167	39	72	26	271	36	238	32
96	22	306	21	224	39	257	18	294	13	140	25
336	41	237	39	251	39	228	34	228	30	191	10
333	40	264	35	115	13	238	30	190	28	337	36
87	14	329	38	206	21	305	17	92	15	205	25
128	23	212	30	237	39	212	33	189	29	86	11
170	26	277	41	264	25	289	39	197	17	202	29
191	29	197	30	329	38	206	32	244	39	337	18
271	36	218	33	212	31	77	22	251	37	268	37
294	33	130	24	277	41	207	25	115	13
228	30	201	11	197	30	296	22	296	22

Решение:

50	50	56	61	61	70	71	71	76	76	80	89
99	99	99	112	112	114	114	124	151	151	154	154
156	171	173	173	174	174	175	175	176	176	181	181
181	185	185	186	189	189	189	190	190	190	191	191
196	196	196	196	202	202	208	208	211	212	212	212
212	217	221	221	222	222	222	228	235	235	235	238
241	248	248	252	255	255	261	261	261	273	273	278
278	280	280	289	290	313	313	314	317	320	320	321
321	321	321	326

После упорядочения значений признака 1 по возрастанию построить для этого признака интервальный вариационный ряд: данные уже упорядочены по возрастанию Х. Строим вариационный ряд:

Х	50	56	61	70	71	76	80	89	99	112	114	124	151	154
N	2	1	2	1	2	2	1	1	3	2	2	1	2	2
Х	156	171	173	174	175	176	181	185	186	189	190	191	196	202
N	1	1	2	2	2	2	3	2	1	3	3	2	4	2
Х	208	211	212	217	221	222	228	235	238	241	248	252	255	261
N	2	1	4	1	2	3	1	3	1	1	2	1	2	3
Х	273	278	280	289	290	313	314	317	320	321	326
N	2	2	2	1	1	2	1	1	2	4	1

Интервальный ряд:

	44-80	80-116	116-152	152-188	188-224	224-260	260-296	296-332
Середина интервала,	62	98	134	170	206	242	278	314
	11	8	3	18	27	11	11	11
	0,11	0,08	0,03	0,18	0,27	0,11	0,11	0,11

Построить многоугольник и гистограмму выборочного распределения признака 1:

Определить числовые характеристики построенного выборочного распределения:

А) выборочную среднюю:

Б) выборочную дисперсию:

В) выборочное среднеквадратичное отклонение:

Для построенного выборочного распределения проверить гипотезу о том, что признак 1 в генеральной совокупности распределен по нормальному закону (уровень значимости = 0,05):

Составим расчетную таблицу:

		=−
62	11	-134,64	-1,8137	0,07703	3,73526	4	12,25
98	8	-98,64	-1,3287	0,16502	8,0024	8	0,00
134	3	-62,64	-0,8438	0,27945	13,5516	14	8,64
170	18	-26,64	-0,3589	0,37406	18,1397	18	0,00
206	27	9,36	0,12608	0,39578	19,1929	19	3,37
242	11	45,36	0,61102	0,33101	16,0518	16	1,56
278	11	81,36	1,09595	0,21882	10,6115	11	0,00
314	11	117,36	1,58089	0,11434	5,54496	6	4,17
Сумма	100				95	96	29,99

Найдем наблюдаемое значение критерия Пирсона: .

По таблице критических точек распределения , по уровню значимости α = 0,05 и числу степеней свободы K =S– 3 = 8 – 3 = 5

находим критическую точку правосторонней области:

Так как нет оснований принимать гипотезу о нормальном распределении генеральной совокупности.

среднеквадратичного отклонения признака 1 в генеральной совокупности, используя для этого первые 21 значений признака 1 в начальной (неупорядоченной) выборке.

Х	У	Х	У
222	34	112	23
89	17	154	26
196	33	175	29
273	39	255	36
190	30	278	33
61	20	212	30
191	25	174	28
80	22	76	14
320	41	173	29
317	40	151	19
71	14

Итак,

Найдем выборочное значение дисперсии:

Ищем критическое значение t при уровне значимости 0,95 и 21-1=20 степенях свободы t= 2,086. Тогда

Доверительный интервал для среднего:

Остальные доверительные интервалы:

Итак, для дисперсии доверительный интервал с вероятностью 0,95 (58; 206,642), для СКО (7,62; 14,38).

Для тех же 21 первых значений признаков 1 и 2 построить уравнение прямой линии регрессии Y (признак 1) на X (признак 2)

и уравнение прямой линии регрессии X На У. Определить коэффициенты корреляции и детерминации и объяснить содержание этих

коэффициентов. Построить графики прямых линий регрессии вместе с заданным корреляционным полем

Составим расчетную таблицу:

I							Y-		X-
1	222	49284	34	1156	7548	31,7756	2,2244	237,1137	-15,1137
2	89	7921	17	289	1513	19,0589	-2,0589	81,3592	7,6408
3	196	38416	33	1089	6468	29,2896	3,7104	227,9517	-31,9517
4	273	74529	39	1521	10647	36,6519	2,3481	282,9238	-9,9238
5	190	36100	30	900	5700	28,7160	1,2840	200,4656	-10,4656
6	61	3721	20	400	1220	16,3818	3,6182	108,8453	-47,8453
7	191	36481	25	625	4775	28,8116	-3,8116	154,6554	36,3446
8	80	6400	22	484	1760	18,1984	3,8016	127,1694	-47,1694
9	320	102400	41	1681	13120	41,1458	-0,1458	301,2479	18,7521
10	317	100489	40	1600	12680	40,8589	-0,8589	292,0859	24,9141
11	71	5041	14	196	994	17,3379	-3,3379	53,8731	17,1269
12	112	12544	23	529	2576	21,2581	1,7419	136,3314	-24,3314
13	154	23716	26	676	4004	25,2739	0,7261	163,8175	-9,8175
14	175	30625	29	841	5075	27,2817	1,7183	191,3036	-16,3036
15	255	65025	36	1296	9180	34,9309	1,0691	255,4378	-0,4378
16	278	77284	33	1089	9174	37,1300	-4,1300	227,9517	50,0483
17	212	44944	30	900	6360	30,8195	-0,8195	200,4656	11,5344
18	174	30276	28	784	4872	27,1861	0,8139	182,1415	-8,1415
19	76	5776	14	196	1064	17,8160	-3,8160	53,8731	22,1269
20	173	29929	29	841	5017	27,0905	1,9095	191,3036	-18,3036
21	151	22801	19	361	2869	24,9870	-5,9870	99,6833	51,3167
	3770	803702	582	17454	116616	582	0	3770	0
	179,524	38271,524	27,714	831,143	5553,143	27,714	0,000	179,524	0,000