Численные методы
ДОМАШНЕЕ ЗАДАНИЕ ПО КУРСУ
«Численные методы»
(для студентов 4 курса каф. № 28, 68)
Содержание
1. Численные методы алгебры.
1.1. Решение алгебраических уравнений
1.2. Определение минимального и максимального собственных значений эрмитовой матрицы
2. Численные методы математического анализа
2.1. Интерполяционные многочлены
2.2. Интерполяционные сплайны
2.3. Аппроксимация функций по методу наименьших квадратов
3. Численные методы решения дифференциальных уравнений. Задача Коши для дифференциального уравнения первого порядка
1. Численные методы алгебры.
1.1. Решение алгебраических уравнений
Тема: Приближенные методы решения алгебраических уравнений. Исследование функции ![]() и решение уравнения
и решение уравнения ![]() .
.
Порядок выполнения:
В соответствии с вариантом задания (номер варианта задания соответствует номеру студента в группе):
1. Исследовать функцию и определить отрезок, содержащий корень уравнения (или начальное приближение для корня), для которого выполняются достаточные условия сходимости одного из итерационных методов.
2. Получить приближенное решение с точностью ![]() , используя методы:
, используя методы:
- бисекции;
- простой итерации;
- касательных
3. Оценить скорость сходимости решения для каждого из методов.
Варианты индивидуальных заданий
Группа №1
|
№ п/п |
|
|
1 |
|
Метод биссекции.
Для метода биссекции необходимо найти интервал изоляции корня, там где функция имеет разные знаки на концах отрезка. Пусть это будет отрезок ![]() . В том случае имеем абсолютную погрешность вычисления корня
. В том случае имеем абсолютную погрешность вычисления корня ![]() при использовании приближенного значения
при использовании приближенного значения ![]() . При каждой итерации метода биссекции абсолютная погрешность уменьшается в 2 раза, требуемое число итераций определим из соотношения
. При каждой итерации метода биссекции абсолютная погрешность уменьшается в 2 раза, требуемое число итераций определим из соотношения
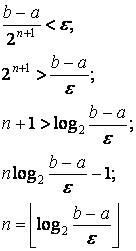
Для изоляции корня используем графический метод.

Имеем два отрезка изоляции корней уравнения: ![]() При
При ![]() корней нет в силу ограниченности функции
корней нет в силу ограниченности функции ![]() сверху значением 1.
сверху значением 1.
Оценим количество необходимых итераций в обоих случаях:
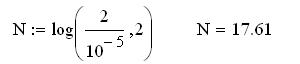
Нужно 17 иттераций.
Так как количество итераций велико, используем для организации вычислений пакет Excel/
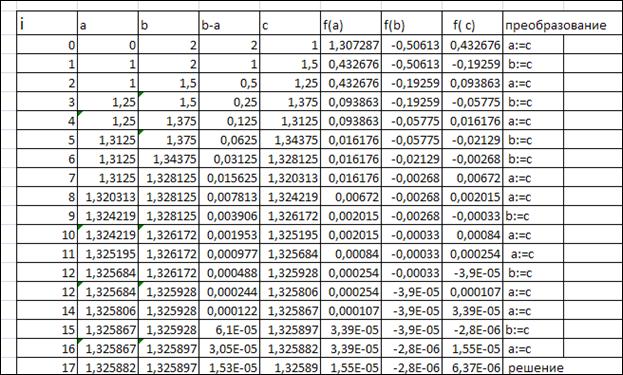
Решение для первого корня получено за 17 иттераций.
![]()
Найдем второй корень
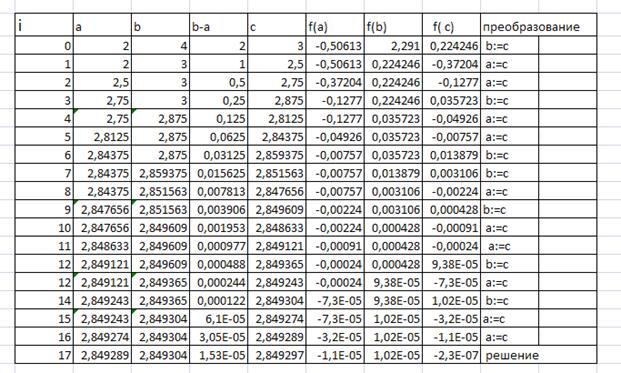
Решение для первого корня получено за 17 иттераций.
![]()
2) Метод простой итерации.
Ищем корень на отрезке ![]()
Изучим знак и модуль первой производной на данном отрезке:
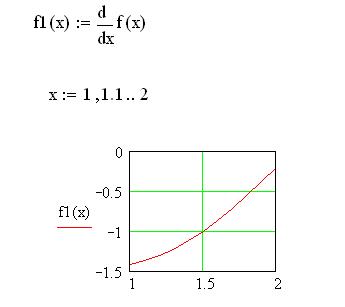
Видим, знак производной отрицательный, модуль меняется от 0.3 до 1.5
Запишем уравнение в эквивалентном виде:
![]()
Рассмотрим отображение
![]()
Оно должно быть сжимающим в данном промежутке. Для выяснения этого вопроса исследуем величину производной функции ![]() на отрезке
на отрезке ![]()

\
Видим, что производная функции ![]()
![]() не превосходит по модулю величины
не превосходит по модулю величины ![]()
Будем выполнять процесс простой итерации по формуле ![]()
При начальном приближении ![]() .Будем использовать оценку погрешности:
.Будем использовать оценку погрешности:
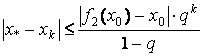 ;
;
Найдем необходимое число приближений;

Т. е. теоретически нужно выполнить ![]() итераций
итераций
Для ускорения решения будем использовать текущую оценку погрешности по текущему приближении. По формуле:
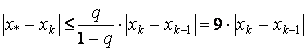
Промежуточные вычисления будем выполнять в пакете Excel:
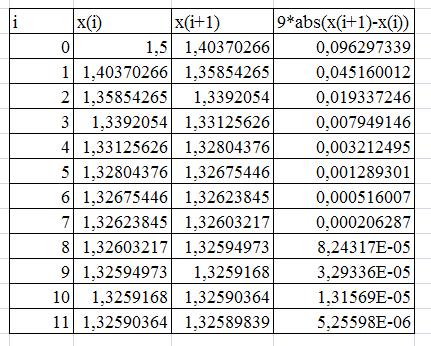
Решение найдено. Потребовалось 11 итераций. Оценка погрешности производилась по текущей разности между последовательными приближениями.
![]()
В) Метод Ньютона
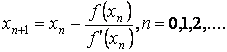
Используем теорию:

Для сходимости по методу Ньютона достаточно, чтобы функция имела разные знаки на концах отрезка, первая и вторая производная не имели нулей и в данном отрезке, в начальной точке функция и вторая производная должны иметь одинаковые знаки. тогда итерации по алгоритму Ньютона сходятся к единственному корню данной функции в указанном отрезке и сходимость квадратичная. Достигаемую точность оцениваем по разности последовательных приближений.
Для изучения знаков производных используем графики:
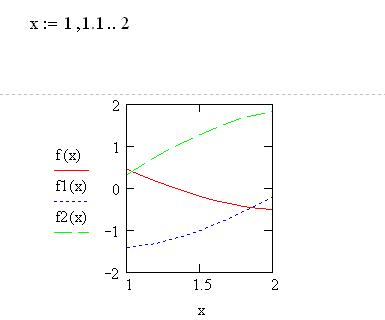
Знаки первой и второй производной на данном отрезке совпадают. В качестве начальной точки используем ![]()
Так как
![]()
В данной начальной точке знак функции и ее второй производной совпадают.
Выполняем итерации по методу Ньютона. Для вычислений используем пакет MathCad/
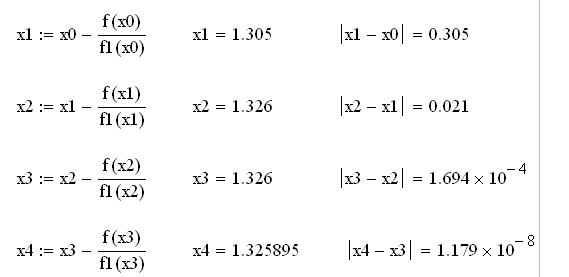
Видим, что для достижения требуемой точности решения потребовалось 4 итерации.
1.2. Определение минимального и максимального собственных значений
Эрмитовой матрицы
Тема: Применение метода поиска максимального по модулю собственного значения для определения минимального и максимального собственных значений эрмитовой матрицы.
Задание: В соответствии с вариантом задания (номер варианта задания соответствует номеру студента в группе) определить минимальное и максимальное собственные значения квадратной симметричной действительной матрицы ![]() с точностью
с точностью ![]() При заданном значении параметра
При заданном значении параметра ![]() >0:
>0:
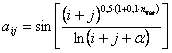 , где
, где ![]() - номер варианта задания.
- номер варианта задания.
Варианты индивидуальных заданий
Группа №1: ![]() = 1.
= 1.
Находим максимальное по модулю собственное число
Применяем степенной метод
1) Формируем матрицу:

2) Формируем начальный вектор
![]()
3) Выполняем 250 итераций по степенному методу
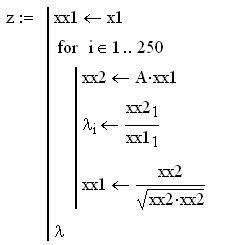
Распечатаем первые 20 итераций

Распечатаем последние 20 итераций

Итерационный процесс сошелся с точностью 0.00001
Ответ: ![]()
Максимальное по модулю собственное значение данной эрмитовой матрицы
Так как оно оказалось отрицательным, то это, фактически, минимальное собственное число.
Проверка по стандартной функции

Ответ получен верно
Найдем максимальное собственное число.
Сделаем необходимок преобразование данной матрицы:

Для полученной матрицы ищем максимальное по модулю собственное число, оно будет равно
![]()
Применяем тот же алгоритм:
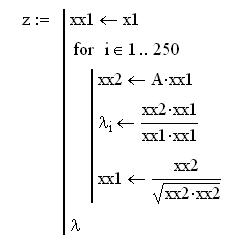
Процесс сошелся.
Распечатаем последние итерации

По данному результату находим максимальное собственное число:
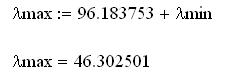
2. Численные методы математического анализа
2.1. Интерполяционные многочлены
Тема: Интерполяционный многочлен Лагранжа.
Задание: В соответствии с вариантом задания (номер варианта задания соответствует номеру студента в группе) для функции ![]() на [A,B] построить интерполяционный многочлен Лагранжа
на [A,B] построить интерполяционный многочлен Лагранжа ![]() по указанному в варианте задания количеству узлов:
по указанному в варианте задания количеству узлов:
1) для равноотстающих узлов
2) для Чебышевской системы узлов.
Построить графики ![]() и
и ![]() .
.
Оценить погрешность (построить графики погрешности). Сравнить результаты в случаях 1) и 2).
Варианты индивидуальных заданий
Группа №1
1) для равноотстающих узлов N = 3, 5;
2) для Чебышевской системы узлов N = 5
|
№ п/п |
|
A |
B |
|
1 |
|
2 |
5 |
Дано
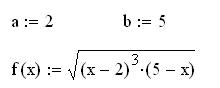
Построение интерполяционного полинома Лагранжа
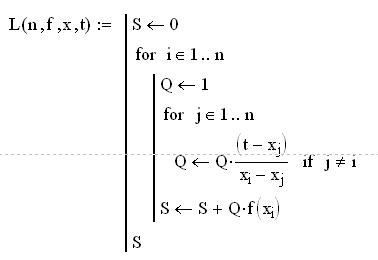
Равномерная сетка с числом узлов ![]()
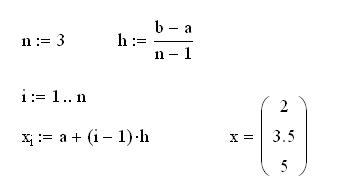
Развернутый вид полинома Лагранжа
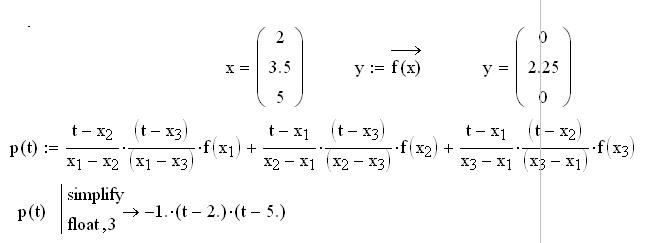
Равномерная сетка с числом узлов ![]()
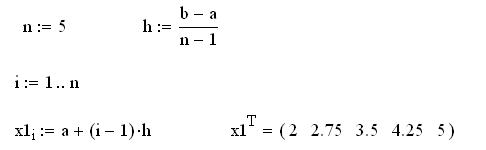
Развернутый вид полинома Лагранжа

Чебышевкая сетка ![]()
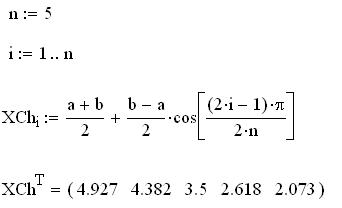
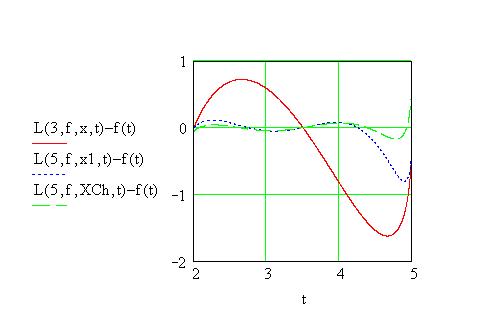
Графики самой функции и трех интерполяционных полиномов:
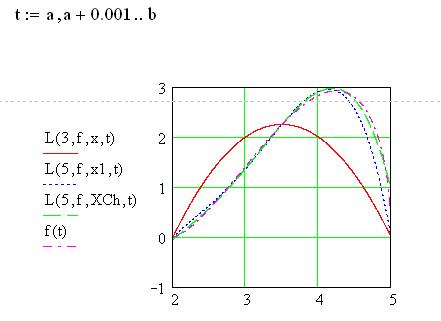
Сравнение ошибок. Графики ошибок.
Вывод: аппроксимативные свойства являются наилучшими для интерполяционного полинома Лагранжа по нулям полинома Чебышева.
2.2. Интерполяционные сплайны
Тема: Построение интерполяционного кубического сплайна.
Задание: В соответствии с вариантом задания (номер варианта задания соответствует номеру студента в группе) построить интерполяционный кубический сплайн для функции ![]() , заданной таблицей, и найти его значение в указанной точке X. Для решения системы алгебраических уравнений применить метод прогонки.
, заданной таблицей, и найти его значение в указанной точке X. Для решения системы алгебраических уравнений применить метод прогонки.
Варианты индивидуальных заданий
Группа №1
|
№ п/п |
|
0.24 |
0.26 |
0.27 |
0.29 |
0.30 |
0.32 |
0.37 |
0.38 |
0.42 |
0.49 |
0.59 |
|
|
1 |
|
0.2449 |
0.3004 |
0.3452 |
0.3714 |
0.4053 |
0.4382 |
0.4777 |
0.5080 |
0.5649 |
0.5784 |
0.6107 |
0.53 |
1) Формирование коэффициентов трехдиагональной линейной системы для нахождения сплайна

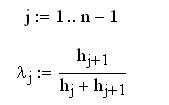

Решение системы уравнений сплайна методом прогонки
А) прямая прогонка

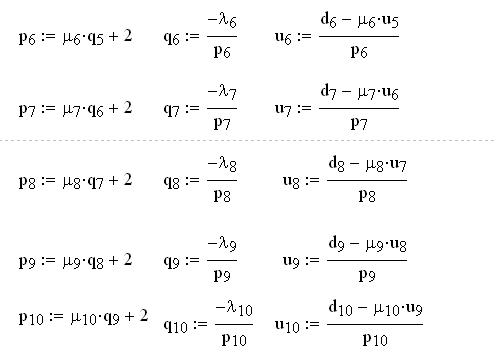

Обратная прогонка
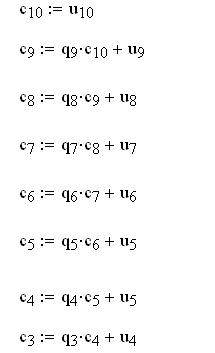

Расчет коэффициентов сплайна
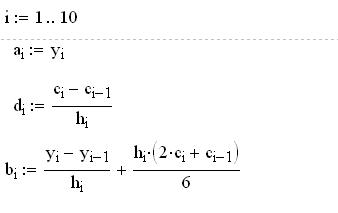
Формирование кубического сплайна

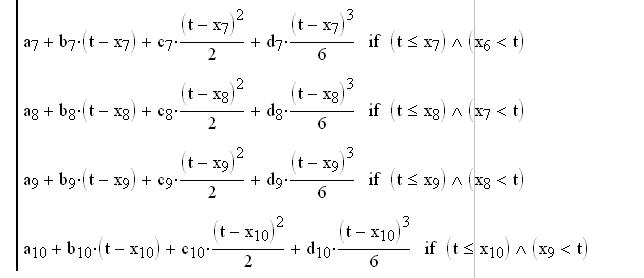
График сплайна

Проверка сплайна по встроенной функции
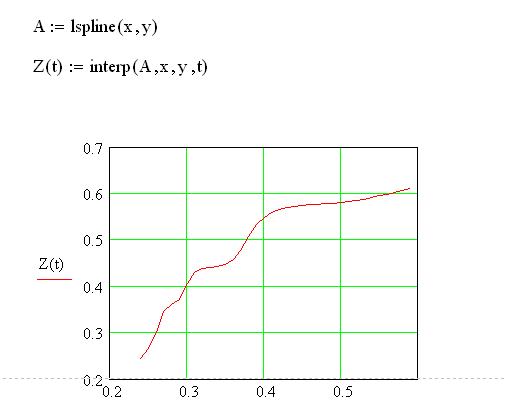
Имеем тот же результат
2.3. Аппроксимация функций по методу наименьших квадратов
Тема: Приближение функций, заданных таблицей, по методу наименьших квадратов.
Задание: Методом наименьших квадратов построить многочлен второй степени, аппроксимирующий функцию, заданную таблично. Найти значение многочлена в заданных точках, абсолютную погрешность в них и среднеквадратическую погрешность, построить графики.
Варианты индивидуальных заданий.
Группа № 1
|
№ п/п |
|
0.24 |
0.26 |
0.27 |
0.29 |
0.30 |
0.32 |
|
1 |
|
0.0792 |
0.1139 |
0.1461 |
0.2041 |
0.2304 |
0.2788 |
Ввод исходных данных

Формирование базисных функций для выполнения квадратичной аппроксимации
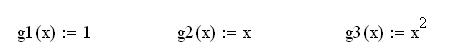
Матрица системы нормальных уравнений для нахождения коэффициентов аппроксимирующего полинома
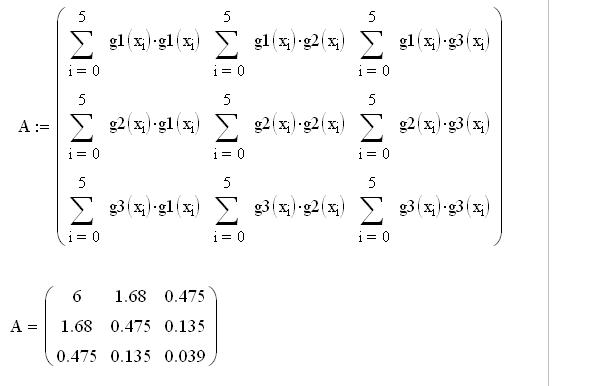
Вектор правых частей системы:

Нахождение коэффициентов аппроксимирующего полинома:
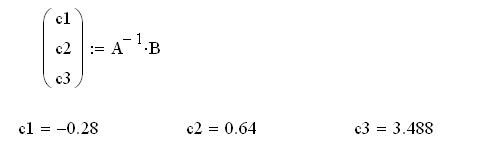
Вид аппроксимирующего полинома второй степени
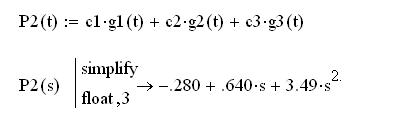
Расчет значений по полиному в данных точках и сравнение с данными значениями

Расчет вектора абсолютных погрешностей аппроксимации в данных точках
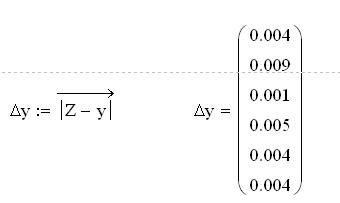
Расчет средней квадратичной ошибки аппроксимации
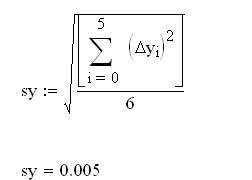
Графики аппроксимирующего полинома и таблично заданной функции

3. Численные методы решения дифференциальных уравнений.
Задача Коши для дифференциального уравнения первого порядка
Тема: Численное решение задачи Коши для ОДУ первого порядка с помощью одношаговых и многошаговых разностных схем.
Задание: Найти приближенные решения задачи Коши
![]() ,
, ![]()
На отрезке [A,B] с шагом H, используя следующие методы:
- метод Эйлера первого порядка точности,
- метод Эйлера второго порядка точности,
- метод Рунге-Кутта второго порядка точности,
- метод Рунге-Кутта четвертого порядка точности,
- метод Адамса второго порядка точности,
- метод Адамса четвертого порядка точности.
Сравнить приближенные решения между собой. Оценить погрешность приближенного решения
Варианты индивидуальных заданий
Группа №1: A = 0; B = 4; H = 0,2
- метод Эйлера первого порядка точности,
- метод Рунге-Кутта четвертого порядка точности,
- метод Адамса второго порядка точности,
|
№ п\п |
|
|
1 |
|
Метод Эйлера первого порядка точности

Метод Рунге четвертого порядка точности

Метод Адамса второго порядка точности
Первый стартовый шаг выполняем по методу Рунге

Нахождение точного решения по встроенной функции
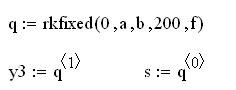
Графический анализ точности полученных решений
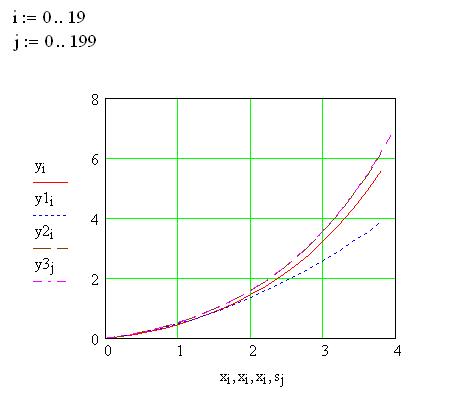
Наибольшую точность имеет метод Адамса
| < Предыдущая | Следующая > |
|---|