32. Ситуации, оптимальные по Парето
Как уже отмечалось, формальное понятие оптимальности призвано отражать различные варианты содержательных представлений об устойчивости, выгодности и справедливости. Можно считать, что устойчивость ситуации проявляется в ее равновесности.
Другой вариант устойчивости ситуации в большей степени, чем равновесность, отражающей черты ее выгодности, состоит в ее оптимальности по Парето[1].
Определение 6. Ситуация Х0 в бескоалиционной игре называется оптимальной по Парето, если не существует ситуации ХÎC, для которой имеет место векторное неравенство
![]() , для всех іÎІ. (5.2)
, для всех іÎІ. (5.2)
Иными словами, в оптимальной по Парето ситуации игроки не могут совместными усилиями увеличить выигрыш кого-либо из них, не уменьшив при этом выигрыш кого-либо другого.
Подчеркнем различие ситуации равновесия от ситуации, оптимальной по Парето: в первой ни один игрок, действуя в одиночку, не может увеличить свой собственный выигрыш; во второй, – все игроки, действуя совместно, не могут (даже нестрого) увеличить выигрыш каждого.
Вопросы об оптимальных по Парето ситуациях решаются в принципе проще, чем аналогичные вопросы о ситуациях равновесия (оптимальных по Нэшу).
Проиллюстрируем графический метод определения ситуаций оптимальных по Парето. На рис. 5.1 изображено множество возможных стратегий Х1,Х2 двух игроков. Каждой точке ХÎC соответствует точка на множестве Н значений функций выигрышей Н1(Х) и Н2(Х) (рис. 5.2).
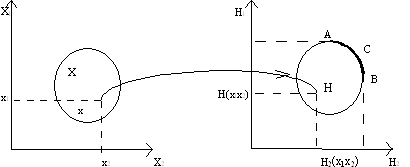
Рис. 5.1 Рис. 5.2
На рис. 5.2 дуга АСВ соответствует множеству ситуаций оптимальных по Парето, так как никакими совместными усилиями Игроков, нельзя увеличить выигрыш одного из них, не уменьшив при этом выигрыш другого.
Определение 7. Игра ![]() называется аффинно эквивалентной игре G, если число игроков
называется аффинно эквивалентной игре G, если число игроков ![]() , стратегии одной игры
, стратегии одной игры ![]() ,
, ![]() (отсюда следует, что игры
(отсюда следует, что игры ![]() и
и ![]() имеют одно и то же множество ситуаций), а функции выигрыша
имеют одно и то же множество ситуаций), а функции выигрыша
![]() ,
,
Где ![]() ,
, ![]() .
.
Различие между двумя аффинно эквивалентными играми по существу состоит в различии начальных капиталов игроков и в соотношениях единиц измерения выигрышей, определяемых соответственно величинами Ci И Ki.
Для однородно аффинно эквивалентных игр Ki=K, i![]() N.
N.
Очевидно, что для антагонистических игр понятия аффинной эквивалентности и однородной аффинной эквивалентности совпадают.
Теорема 1. Всякая бескоалиционная игра с постоянной суммой аффинно эквивалентна некоторой игре с нулевой суммой.
Теорема 2. Аффинно эквивалентные игры имеют одни и те же оптимальные по Парето ситуации.
Рассмотрим пример для нахождения ситуации оптимальной по Парето.
Пример 2. Игра “Дилемма заключенного”
Каждый из двух игроков располагает двумя стратегиями: А2 и В2 – стратегии агрессивного поведения, а А1 и В1 – миролюбивое поведение. Предположим, что “мир” (оба игрока миролюбивы) лучше для обоих игроков, чем “война”. Случай, когда один игрок агрессивный, а другой миролюбивый, выгоднее агрессору. Пусть матрицы выигрышей игроков 1 и 2 в данной биматричной игре имеют вид
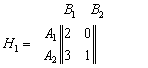 ,
, ![]()
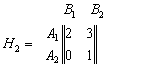 .
.
Для обоих игроков агрессивные стратегии А2 и В2 доминируют мирные стратегии А1 и В1. Таким образом, единственное равновесие в доминирующих стратегиях имеет вид (А2,В2), т. е. постулируется, что результатом некооперативного поведения является война. В то же время исход (А1,В1) (мир) дает больший выигрыш для обоих игроков. Таким образом, некооперативное эгоистическое поведение вступает в противоречие с коллективными интересами. Коллективные интересы диктуют выбор мирных стратегий. В то же время, если игроки не обмениваются информацией, война является наиболее вероятным исходом.
В данном случае ситуация (А1, В1) является оптимальной по Парето. Однако эта ситуация неустойчива, что ведет к возможности нарушения игроками установленного соглашения. Действительно, если первый игрок нарушит соглашение, а второй не нарушит, то выигрыш первого игрока увеличится до трех, а второго упадет до нуля и, наоборот. Причем, каждый игрок, не нарушающий соглашение, теряет больше при нарушении соглашения вторым игроком, нежели в том случае, когда они оба нарушают соглашение.
Как видим, в отличие от примера 1 (игра “семейный спор”), где кооперация игроков была им выгодна, в этом примере кооперация не выгодна для игроков.
| < Предыдущая | Следующая > |
|---|