03.3. Дисперсия и среднее Квадратическое отклонение
Среднее значение, или математическое ожидание, случайной величИНы в ряде вопросов является достаточной характеристикой изучаемой случайной величины. Но бывает так, что одно среднее значение не дает практически исчерпывающей характеристики случайной величины, а требуется еще знать, сколь велики отклонения отдельных значений случайной величины от ее среднего значения.
Например, вычисляя какую-либо физическую постоянную некоторого вещества (теплоемкость, теплопроводность, электропроводимость и т. Д.) опытным путем, мы фиксируем полученные отдельные показания измерительных приборов путем K-Кратного повторения испытания.
Аналогично мы встречаемся со случайной величиной, когда, например, по данным статистического наблюдения изучается: средний рост или вес человека в определенной группе, средняя выработка ткани (в метрах) рабочим ткацкого цеха за нормальный рабочий день, средняя заработная плата рабочего отдельного цеха завода, среднесуточный пробег одной грузовой машины (по данным о пробеге всех машин автобазы) и т. д.
Во всех таких случаях результат опыта или наблюдения может считаться удачным, если 
определяется при незначительных отклонениях 
.
Поэтому возникает необходимость введения еще понятия отклонения случайной величины от ее среднего значения 
. Это отклонение характеризует рассеяние случайной величины.
Пусть одно и то же среднее значение в опытном вычислении при 5 измерениях является для первой серии измерений результатом одних отдельных значений (рис. 9), а для второй серии измерений — результатом других отдельных значений (рис. 10).
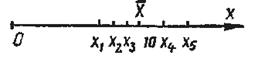
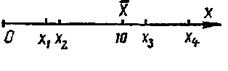
Рис. 9 Рис. 10
Первая серия вычислений характеризуется малым рассеянием случайной величины по сравнению с большим рассеянием ее при второй серии вычислений.
|
I |
|
II | |||||||||
|
|
7 |
8 |
9 |
12 |
14 |
|
|
4 |
5 |
12 |
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Числовые данные распределения таковы:
I. 
II. 
Таким данным распределения самой случайной величины и ее среднему значениЮ соответствуют следующие данные Относительно Отклонений :
|
I |
II | ||||||||||
|
|
-3 |
-2 |
-1 |
2 |
4 |
|
-6 |
-5 |
2 |
7 | |
|
|
|
|
|
|
|
|
|
|
|
|
В этих таблицах роль случайной величины играет уже отклонение значений 
от среднего. При этом распределение отклонений во второй серии характеризуется бОЛЬшиМи амплитудами.
Среднее значение (математическое ожидание) отклонения случайной величины от ее среднего значения всегда равно нулю.
Действительно, 
Этот же результат, конечно, получается и Непосредственно в Рассмотренных примерах:
I. 
II. 
Так как среднее значение отклонения всегда равно нулю, то оно не может дать характеристики рассеяния случайной величины. Этой цели может служить среднее значение абсолютной величины отклонения 
:
,
Которое называется Средним отклонением.
При стрельбе, например, именно эти величины служат показателями близости точек попаданий к цели.
Для приведенных нами примеров средние отклонения определяются по таблицам распределения:
|
I |
II | |||||||||
|
|
1 |
2 |
3 |
4 |
|
2 |
5 |
6 |
7 | |
|
|
|
|
|
|
|
|
|
|
|
Отсюда находим средние отклонения:
I. 
II. 
Для характеристики рассеяния случайной величины бывает выгодно пользоваться срЕДниМ значением квадрата отклонения, которое называется Дисперсией случайной величины D(X):
.
Если применить принятое еще обозначение 
, то запИСь дисперсии (математического ожидания квадрата отклонения случайной величины от ее среднего значения) дает
.
Не выполняя суммирования, можно Преобразовать Дисперсии в общем виде.
Так как
То
Применяя свойство 2°, п. 3.2, имеем
.
Но
А 
(свойство 1°, п. 3.2).
Поэтому
, или 
.
Таким образом, Дисперсия случайной величины РавнА Разности Между средним значением (математическим ожиданием) квадратА Случайной величины и квадратом ее среднего значения.
Дисперсия 
дает представление о том, чему В Среднем равен квадрат отклонения . Для оценки же самой величины отклонения служит 
, т. Е. Среднее Квадратическое Отклонение:
.
Эта величина, наряду со средним отклонением 
может служить вероятностной характеристикой отклонений случайной величины от ее среднего значения.
Применение среднего Квадратического отклонения для характеристики степени рассеяния случайной величины более выгодно, чем применение среднего отклонения:
А) обращение к среднему Квадратическому отклонению исключает вычисления с абсолютными величинами, что оказывается часто сложным;
Б) среднее отклонение, как ниже устанавливается, обычно меньше, но никогда не превышает среднего квадратического отклонения, а это значит, что среднее Квадратическое отклонение заметнее выражает имеющееся рассеяние случайной величины, чем среднее отклонение;
В) если рассматривается сумма независимых случайных величин, то для этой суммы действует правило сложения дисперсий (см. ниже), что соответственно упрощает отыскание среднего квадратического отклонения.
Найдем для рассмотренных нами примеров случайных величин средние Квадратические отклонения.
Из таблиц распределения квадратов отклонений
|
I |
II | |||||||||
|
|
1 |
4 |
9 |
16 |
|
4 |
25 |
36 |
49 | |
|
|
|
|
|
|
|
|
|
|
|
Определим дисперсии:
I. 
II. 
Такие же результаты должно дать ИсполЬзование формулы
.
Здесь имеем:
|
I |
II | ||||||||||
|
|
49 |
64 |
81 |
144 |
196 |
|
16 |
25 |
144 |
289 | |
|
|
|
|
|
|
|
|
|
|
|
|
Что дает для случайной величины I
Отсюда 
Для случайной величины II получаем
Откуда 
Таким образом, средние квадратические отклонения составляют: для I величины 
для II величины 
в сравнении со средними отклонениями, соответственно равными 2.4 и 4.4.
Мы видим, что обе характеристики отклонений от среднего значения случайной величины [и среднее отклонение , и среднее квадратическое отклонение ] показывают, что случайная величина II рассеяна в большей степени, чем случайная величина I.
Вместе с тем полученные для обеих случайных величин результаты говорят о том, что Среднее отклонение оказалось меньшЕ Среднего квадратического отклонения. Это связано с общим правилом: Среднее значение квадрата любой случайной величины всегда не меньше, чем квадрат среднего значения этой случайной величины.
Дадим вывод этого правила в общем виде. Составим равенство из двух выражений для D(X):
.
Правая часть здесь неотрицательна, так как неОтрицательно Каждое слагаемое вида 
. Поэтому и
или 
Если 
рассматривать как среднее значение квадрата случайной величины 
, то 
. Это значит, что Дисперсия случайной величины не меньше, чем квадрат Среднего отклонения этой величины, а ОтсюДа справедливо неравенство
ВЫВедем правило сложения дисперсий.
ДисперсИя суммы, независимых величин Х и Y РавнА сумме их Дисперсий.
Пусть даны независимые случайные величины Х и Y, МатематИЧеские ожидания которых М(Х)=А и M(Y)=B.
По определению дисперсии 
Поэтому
Выполняя соответствующие преобразования, получим
Применяя свойство 2° о математическом ожидании суммы случайных величин, получим
Где
И
Для третьего слагаемого имеет место свойство 3° о Математическом ожидании проИЗведения:
Введенное правило сохраняет свою силу для суммы любого КОНечного числа попарно независимых случайных величин.
Если X, Y, Z, ..., U, V — Попарно независимые случайные величины, то дисперсия суммы этих величин равна сумме Дисперсий ЕЕ отдельных слагаемых:
.
Пример 8. При ознакомлении с асимптотической Формулой биноминального распределения и при доказательстве Интегральной Теоремы Лапласа мы оперировали с величиной
.
Показать, что эта величина определяет среднее квадратическое отклонение числа (M) появлений События А в N независимых испытаниях.
Решение. Найдем дисперсию случайной величины Т в биномиальном распределении при П испытаниях, пользуясь формулой 
, которая для отдельного испытания дает:
1) из таблицы распределения для 
|
|
1 |
0 |
|
|
P |
Q |
Имеем
2) из таблицы распределения для 
|
|
1 |
0 |
|
|
P |
Q |
Имеем
Отсюда 
.
Это — дисперсия числа в каждом отдельном испытании, а поэтому для П испытаний используем, на основании правила сложения дисперсий, операцию суммирования
,
Которая в силу полного совпадения всех слагаемых дает 
.
Отсюда среднее Квадратическое отклоненИЕ
.
| < Предыдущая | Следующая > |
|---|
