11.1. Понятие производной
Рассматривая бесконечно малые функции, мы сравнивали их между собой путем нахождения предела их отношения. Однако необходимость такой процедуры возникает даже тогда, когда изучаются свойства одной заданной функции ![]() . При изучении мгновенной скорости, а также углового коэффициента касательной к графику функции мы столкнулись c рассмотрением отношения приращения функции к приращению аргумента при стремлении к нулю приращения аргумента. Таких задач существует великое множество. Неочевидность их решения связана с принципиальной трудностью: даже для непрерывных функций возникает необходимость раскрытия неопределенности
. При изучении мгновенной скорости, а также углового коэффициента касательной к графику функции мы столкнулись c рассмотрением отношения приращения функции к приращению аргумента при стремлении к нулю приращения аргумента. Таких задач существует великое множество. Неочевидность их решения связана с принципиальной трудностью: даже для непрерывных функций возникает необходимость раскрытия неопределенности ![]() . Раскрыть эту неопределенность порой бывает очень непросто.
. Раскрыть эту неопределенность порой бывает очень непросто.
Возможно, гениальность Ньютона, давшего понятие мгновенной скорости, состояла как раз в том, что от умозрительного восприятия перемещения за бесконечно малый промежуток времени ему удалось перейти к пределу отношения приращения пути к приращению времени, породившего это изменение пути. Эта же идея стала основной в определении углового коэффициента касательной к кривой и была реализована Лейбницем. Именно понятие предела отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, введенное этими учеными в конце XVII века в связи с рассмотрением указанных задач, приобрело стремительное продолжение. Отыскание этого предела, названного производной, позволило изучить важнейшие свойства функциональных зависимостей, создать теорию дифференциальных уравнений, описывающую самые разнообразные процессы реального мира, развить новые математические идеи.
ПРОИЗВОДНАЯ функции ![]() в точке
в точке ![]() есть конечный предел отношения приращения функции
есть конечный предел отношения приращения функции ![]() к вызвавшему его приращению аргумента
к вызвавшему его приращению аргумента ![]() , когда приращение аргумента стремится к нулю (
, когда приращение аргумента стремится к нулю (![]() может принимать как положительные, так и отрицательные значения).
может принимать как положительные, так и отрицательные значения).
Принято обозначение
![]() ,
,
И функция, имеющая производную, называется дифференцируемой.
|
Приведите примеры функций, отражающие другие физические процессы, и укажите физический смысл производных этих функций. |
Операция нахождения производной функции называется ДИФФЕРЕНЦИРОВАНИЕМ. Сама производная ![]() также представляет собой функцию, определенную при тех значениях х, при которых
также представляет собой функцию, определенную при тех значениях х, при которых ![]() дифференцируема.
дифференцируема.
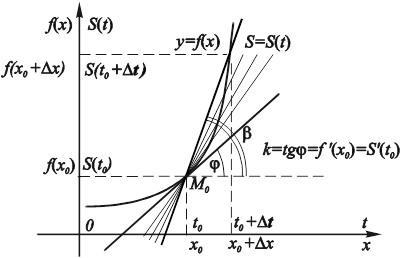
Геометрический смысл производной функции ![]() в точке
в точке ![]() становится понятным: ее значение есть угловой коэффициент касательной (рис.11.1), проведенной к графику функции в точке
становится понятным: ее значение есть угловой коэффициент касательной (рис.11.1), проведенной к графику функции в точке ![]() .
.
![]() .
.
Если же данная кривая – график функции ![]() , определяющей зависимость пути S материальной точки от времени t, то величина
, определяющей зависимость пути S материальной точки от времени t, то величина ![]() – мгновенная скорость движения в момент времени
– мгновенная скорость движения в момент времени ![]() (рис. 11.1).
(рис. 11.1).
|
Рис. 11.1. Геометрический и механический смысл Производной в точке М0. |
Найдем в качестве примера мгновенную скорость свободного падения тела в момент времени ![]() при его свободном падении с высоты H:
при его свободном падении с высоты H:
![]() .
.
Имеем:

| < Предыдущая | Следующая > |
|---|