07.1. Определённый интеграл. Условия существования определенного интеграла. Определение определенного интеграла
Пусть функция F(X) задана на отрезке [А, B]. Разобьем отрезок [А, B] на П произвольных частей точками:
![]()
Выберем в каждом из частичных отрезков [Xi, Xi+1] произвольную точку ξI:
![]()
Теперь образуем сумму произведений:
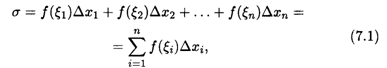
Которую будем называть Интегральной суммой для функции F(X) на отрезке [А, b]. Геометрический смысл величины σ указан на рис. 7.1: это сумма площадей прямоугольников с основаниями ΔXi и высотами F(ξI) (I = 1, 2, ..., П).
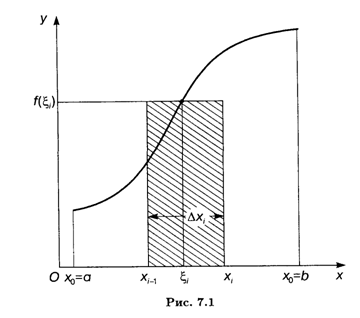
Введем еще одну величину. Обозначим через λ длину макcимального частичного отрезка данного разбиения:
![]()
Определение. Конечный предел I интегральной суммы σ при λ → 0, если он существует, называется Определенным интегралом от функции F(X) по отрезку [А, B]:
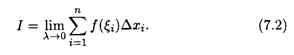
Определенный интеграл обозначается символом
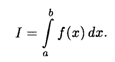
Если определенный интеграл (7.2) существует, то функция F(X) называется Интегрируемой на отрезке [А, b], числа А и B — соответственно Нижним и верхним пределами интегрирования, F(X) — подынтегральной функцией, х — переменной интегрирования.
Величина определенного интеграла, согласно данному выше определению, однозначно определяется видом функции F(X) и числами А и B. Определенный интеграл не зависит от обозначения переменной интегрирования, т. е.
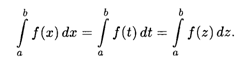
| < Предыдущая | Следующая > |
|---|