5.2. Метод вращения

Любую действительную, симметричную матрицу A можно привести к виду A = U ∙D ∙U–1 , где U – ортогональная матрица (U –1 = U T ),

D – диагональная матрица,

Где λI – собственные значения матрицы A.

Следовательно, имеем U–1 ∙A ∙U = D.

На этом свойстве матрицы основан метод вращения: если некоторым ортогональным преобразованием V свести матрицу A к диагональной: , То собственные значения матриц совпадают.

Таким образом, нужно построить последовательность ортогональных преобразований, позволяющих неограниченно уменьшать модули недиагональных элементов матрицы A. Обозначим . Пусть с помощью преобразования подобия ортогональными матрицами построена последовательность матриц. При этом если , то процесс является монотонным.

Итак, по заданной матрице A будем строить последовательность Ak так, чтобы Ak-1 находилась через Ak при помощи преобразования подобия со следующей матрицей вращения:

Пусть нашли . Найдем . Пусть это будет , K<L (I, J = 1,…,M), и выбираем угол по формуле

.

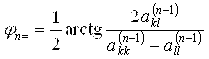Строится ортогональная матрица Vn, которая отличается от единичной матрицы E только элементами:

,

,

И делается преобразование подобия

.

При этом матрицы A(N-1) и Vn A(N-1) = B отличаются лишь K –й и L –Й строками, т. к. эти матрицы B являются линейными комбинациями тех же строк матрицы A(N-1):

,

.

Аналогично K –й и L -Й столбцы матрицы A(N):

,

.

Элементы являются приближенными к собственным числам λi матрицы A, а столбцы матрицы

Являются приближенными к собственным векторам матрицы A. При этом имеет место оценка погрешности

.

< Предыдущая		Следующая >