05. Приближенное вычисление определенного интеграла
При вычислении значения определенного интеграла в экономическом анализе часто нет необходимости вычислять точное значение, тем более что подынтегральное выражение может иметь слишком сложную форму. Поэтому, часто достаточно использовать приближенные методы. Рассмотрим два из них – метод прямоугольников и метод трапеций. Графически метод прямоугольников можно проиллюстрировать следующим образом:
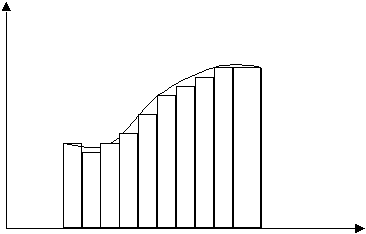
Известно, что значение определенного интеграла равно площади криволинейной трапеции ограниченной сверху графиком подынтегрального выражения, слева и справа границами интервала. Если разбить исследуемый интервал на N прямоугольников, то очевидно, что их суммарная площадь будет приближенно равна площади криволинейной трапеции. Возможны, в этом случае, два варианта – прямоугольники начинают строить слева, и в этом случае общая формула прямоугольников выглядит как
 ,
,
Где h – шаг изменения по x на интервале [a;b]
![]() ,
,
N – количество интервалов,
![]() - значения подынтегрального выражения в точках интервала с шагом h.
- значения подынтегрального выражения в точках интервала с шагом h.
Если же начать строить прямоугольники справа, то
 ,
,
Метод трапеций отличается от метода прямоугольников единственно тем, что вместо прямоугольников строятся трапеции. Очевидно, что при построении трапеций точность вычисления повышается. Формула трапеций выглядит как
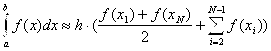
Например, рассмотрим все три способа вычисления определенного интеграла на примере
![]()
Точное значение интеграла, определенное по формуле Ньютона-Лейбница равно 9. Зададимся величиной шага 0,2 и подсчитаем значение по формулам левых и правых прямоугольников и по формуле трапеций. По формуле левых прямоугольников
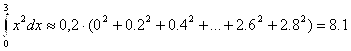
Аналогично можно подсчитать по остальным формулам. Результаты сведем в таблицу.
|
X |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
1,2 |
1,4 |
1,6 |
1,8 |
2 |
2,2 |
2,4 |
2,6 |
2,8 |
3 |
|
F |
0 |
0 |
0,2 |
0,4 |
0,6 |
1 |
1,4 |
2 |
2,6 |
3,2 |
4 |
4,8 |
5,8 |
6,8 |
7,8 |
9 |
|
Левых прямоугольников |
Правых прямоугольников |
Трапеций | ||||||||||||||
|
8,1 |
9,9 |
9,02 |
Очевидно, что значение, подсчитанное по формуле трапеций наиболее близко к точному. Однако достаточно часто не требуется высокая точность вычислений и можно использовать две другие формулы.
| < Предыдущая | Следующая > |
|---|