2.2.6. Полиномы Жегалкина
Полином вида ![]() , где
, где ![]() - элементарные конъюнкции различных переменных без отрицаний (среди
- элементарные конъюнкции различных переменных без отрицаний (среди ![]() может быть константа 1), называется Полиномом Жегалкина.
может быть константа 1), называется Полиномом Жегалкина.
Например, ![]() .
.
Теорема (Жегалкин). Любая булева функция представляется в виде полинома Жегалкина, причем единственным образом с точностью до порядка следования элементарной конъюнкции (слагаемых) и до порядка следования переменных в элементарных конъюнкциях.
Доказательство. Если функция ![]() , то полиномом Жегалкина для данной функции является константа 0. В остальных случаях представим функцию в виде СДНФ:
, то полиномом Жегалкина для данной функции является константа 0. В остальных случаях представим функцию в виде СДНФ: 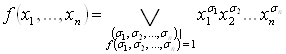 .
.
Преобразуем СДНФ в полином Жегалкина. Прежде всего, все знаки дизъюнкции можно заменить на знак суммы по модулю 2 :
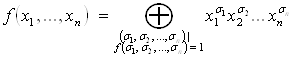 .
.
Это можно сделать по следующей причине: дизъюнкция ![]() (проверить).
(проверить).
Если ![]() и
и ![]() заменить элементарными конъюнкциями из СДНФ, то получим
заменить элементарными конъюнкциями из СДНФ, то получим ![]() , так как
, так как ![]() . Действительно
. Действительно ![]() и
и ![]() имеют одинаковые наборы переменных, которые отличаются только расстановкой отрицания, поэтому в произведении
имеют одинаковые наборы переменных, которые отличаются только расстановкой отрицания, поэтому в произведении ![]() найдется переменная
найдется переменная ![]() , которая встречается с отрицанием и без отрицания. А конъюнкция таких переменных: равна нулю:
, которая встречается с отрицанием и без отрицания. А конъюнкция таких переменных: равна нулю: ![]() .
.
Далее в полученной формуле преобразуем отрицания по формуле: ![]() (проверить). После этого останется раскрыть скобки, что можно сделать ввиду следующего дистрибутивного закона:
(проверить). После этого останется раскрыть скобки, что можно сделать ввиду следующего дистрибутивного закона: ![]() (проверить). После раскрытия всех скобок мы получим сумму элементарных конъюнкций без отрицаний. Если среди полученных конъюнкций есть одинаковые, то все их (за исключением, может быть, одной из группы одинаковых) можно убрать по следующему правилу:
(проверить). После раскрытия всех скобок мы получим сумму элементарных конъюнкций без отрицаний. Если среди полученных конъюнкций есть одинаковые, то все их (за исключением, может быть, одной из группы одинаковых) можно убрать по следующему правилу: ![]() . В итоге получим полином Жегалкина.
. В итоге получим полином Жегалкина.
Чтобы убедиться в единственности полинома Жегалкина для данной функции, подсчитаем количество различных полиномов от ![]() переменных. Заметим, что можно составить
переменных. Заметим, что можно составить ![]() элементарных конъюнкций из
элементарных конъюнкций из ![]() переменных без отрицания. (Действительно для каждой из
переменных без отрицания. (Действительно для каждой из ![]() Переменной имеется две возможности: данная переменная входит в данную конъюнкцию или нет). Далее для каждой конъюнкции существует также 2 возможности: она входит в данный полином Жегалкина или нет. Поэтому количество различных полиномов Жегалкина равно
Переменной имеется две возможности: данная переменная входит в данную конъюнкцию или нет). Далее для каждой конъюнкции существует также 2 возможности: она входит в данный полином Жегалкина или нет. Поэтому количество различных полиномов Жегалкина равно ![]() , т. е. ровно столько, сколько существует различных булевых функций от
, т. е. ровно столько, сколько существует различных булевых функций от ![]() переменных. Из данного совпадения вытекает единственность полинома Жегалкина. Действительно, если бы какую-то функцию можно было представить двумя или несколькими полиномами Жегалкина, то некоторые функции нельзя было бы представить полиномом Жегалкина. А уже доказано, что любую функцию можно представить полиномом Жегалкина.
переменных. Из данного совпадения вытекает единственность полинома Жегалкина. Действительно, если бы какую-то функцию можно было представить двумя или несколькими полиномами Жегалкина, то некоторые функции нельзя было бы представить полиномом Жегалкина. А уже доказано, что любую функцию можно представить полиномом Жегалкина.
Пример. Пусть функция ![]() задана следующей таблицей истинности.
задана следующей таблицей истинности.
|
|
|
|
|
Строим полином Жегалкина сразу Преобразовывая соответствующую СДНФ:
| |
|
0 |
0 |
0 |
0 | ||
|
0 |
0 |
1 |
1 | ||
|
0 |
1 |
0 |
1 | ||
|
0 |
1 |
1 |
0 | ||
|
1 |
0 |
0 |
0 | ||
|
1 |
0 |
1 |
0 | ||
|
1 |
1 |
0 |
1 | ||
|
1 |
1 |
1 |
1 |
| < Предыдущая | Следующая > |
|---|