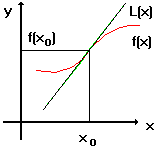6.3. Выпуклость и вогнутость функции, точки перегиба
Пусть функция ![]() дифференцируема дважды в интервале
дифференцируема дважды в интервале ![]() . Проведем касательную
. Проведем касательную ![]() к графику функции в точке
к графику функции в точке ![]()
![]() , ее уравнение имеет вид
, ее уравнение имеет вид
![]() .
.
Обозначим правую часть уравнения ![]() :
: ![]() .
.
Определение 1. Функция ![]() называется Выпуклой вверх (Выпуклой вниз - Вогнутой) на
называется Выпуклой вверх (Выпуклой вниз - Вогнутой) на ![]() , если
, если ![]()
![]() .
.
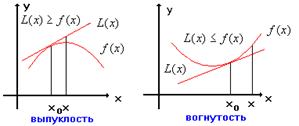
Теорема. Если функция ![]() дважды дифференцируема на интервале
дважды дифференцируема на интервале ![]() и
и ![]()
![]() , то она выпукла (вогнута) на
, то она выпукла (вогнута) на ![]() .
.
Доказательство. Применим к разности ![]() теорему Лаг-ранжа дважды
теорему Лаг-ранжа дважды
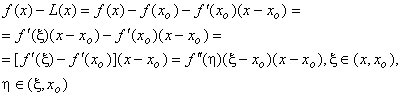
При ![]() имеем
имеем ![]() . Поэтому знак разности
. Поэтому знак разности ![]() совпадает со знаком
совпадает со знаком ![]() , что записывают так:
, что записывают так:
![]() .
.
Поэтому, если ![]() на
на ![]() , то
, то ![]() - выпуклость, если
- выпуклость, если ![]() , то
, то ![]() - вогнутость.
- вогнутость.
|
|
Определение 2. Если разность ![]() меняет знак при переходе через точку
меняет знак при переходе через точку ![]() , то она называется точкой перегиба Функ-ции
, то она называется точкой перегиба Функ-ции ![]() .
.
Необходимое условие в точке перегиба.
В точке ![]() перегиба функции
перегиба функции ![]() либо
либо ![]() , либо не существует
, либо не существует ![]() .
.
Доказательство. Запишем формулу Тейлора для разности ![]() :
:
![]() .
.
Поскольку ![]() , то
, то ![]() . Чтобы знак разности
. Чтобы знак разности ![]() изменился при переходе через точку
изменился при переходе через точку ![]() следует положить
следует положить ![]() .
.
Первое достаточное условие наличия перегиба.
Если функции ![]() дважды дифференцируема в окрестности точки
дважды дифференцируема в окрестности точки ![]() и
и ![]() меняет знак при переходе через точку
меняет знак при переходе через точку ![]() , то
, то ![]() является точкой перегиба.
является точкой перегиба.
Доказательство. Применим к разности ![]() дважды теорему Лагранжа, получим
дважды теорему Лагранжа, получим ![]() . Откуда следует, что, если
. Откуда следует, что, если ![]() меняет знак при переходе через точку
меняет знак при переходе через точку ![]() , то меняет знак разность
, то меняет знак разность ![]() .
.
Пример 1. Найти интервалы выпуклости и вогнутости, точки пере-гиба функции ![]() .
.
Составим уравнение ![]() :
:
![]() .
.
Отсюда получим интервалы: ![]() .
.
Результаты удобно свести в таблицу
|
Интер-вал |
|
|
|
|
|
|
Знак |
+ |
- |
+ | ||
|
Вогнутость |
перегиб |
Выпуклость |
Перегиб |
Вогнутость |
Из таблицы ясно видно, что точки ![]() являются точками перегиба.
являются точками перегиба.
Второе достаточное условие наличия перегиба.
Если функции ![]() дважды дифференцируема в окрестности точки
дважды дифференцируема в окрестности точки ![]() и
и ![]() , то
, то ![]() является точкой пере-гиба.
является точкой пере-гиба.
Доказательство. Запишем формулу Тейлора для разности ![]() с учетом того, что
с учетом того, что ![]() :
:
![]() .
.
При ![]() :
: ![]() . Посколь-ку величина
. Посколь-ку величина ![]() меняет знак при переходе через точку
меняет знак при переходе через точку ![]() , то разность
, то разность ![]() также меняет знак. Откуда следует, что
также меняет знак. Откуда следует, что ![]() является точкой перегиба.
является точкой перегиба.
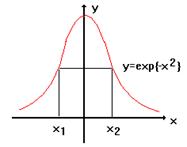
Пример 2. Найти точки перегиба функции ![]() .
.
Используем результаты примера 1
![]() ,
,
![]() .
.
Откуда следует, что ![]() являются точками перегиба.
являются точками перегиба.
| < Предыдущая | Следующая > |
|---|