4.10. Производные от параметрически заданной функции
Теорема. Пусть функции ![]() и
и ![]() дифференцируемы в точке
дифференцируемы в точке ![]() и
и ![]() , тогда параметрически заданная функция
, тогда параметрически заданная функция ![]() дифференцируема в точке
дифференцируема в точке ![]() , причем
, причем
![]() . (1)
. (1)
Если ![]() и
и ![]() дважды дифференцируемы в точке
дважды дифференцируемы в точке ![]() , то существует вторая производная
, то существует вторая производная
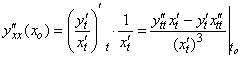 . (2)
. (2)
Доказательство. По правилу дифференцирования сложной функции ![]() , а по правилу дифференцирования обратной функции
, а по правилу дифференцирования обратной функции ![]() . Откуда следует формула (1) теоремы. Получим формулу (2)
. Откуда следует формула (1) теоремы. Получим формулу (2)
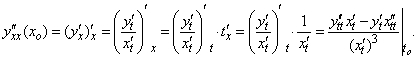 Пример. Вычислить первую и вторую производные функции, заданной уравнением циклоиды
Пример. Вычислить первую и вторую производные функции, заданной уравнением циклоиды
![]() .
.
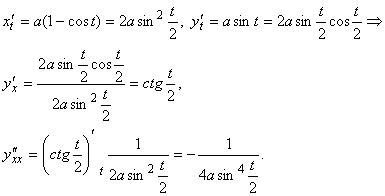
| < Предыдущая | Следующая > |
|---|