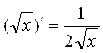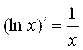4.06. Производная сложной функции
Пусть ![]() , а
, а ![]() – любые две дифференцируемые функции своих аргументов. Тогда функция
– любые две дифференцируемые функции своих аргументов. Тогда функция ![]() – так называемая Сложная функция от X (она представляет собой функцию от функции). Найдем ее производную
– так называемая Сложная функция от X (она представляет собой функцию от функции). Найдем ее производную ![]() (производную от Y по X). Для этого дадим аргументу X некоторое приращение
(производную от Y по X). Для этого дадим аргументу X некоторое приращение ![]() , то есть перейдем от X к
, то есть перейдем от X к ![]() . Приращение
. Приращение ![]() величины X вызовет некоторое приращение
величины X вызовет некоторое приращение ![]() величины U, а то, в свою очередь, вызовет некоторое приращение
величины U, а то, в свою очередь, вызовет некоторое приращение ![]() величины Y. Так как функции
величины Y. Так как функции ![]() и
и ![]() являются, по условию, дифференцируемыми функциями своих аргументов, то они являются и непрерывными функциями своих аргументов (см. теорему в § 1). То есть при
являются, по условию, дифференцируемыми функциями своих аргументов, то они являются и непрерывными функциями своих аргументов (см. теорему в § 1). То есть при ![]() и
и ![]() , и
, и ![]() . А тогда, согласно (1.5), получаем:
. А тогда, согласно (1.5), получаем:
 .
.
Итак, если ![]() – сложная функция от X, то
– сложная функция от X, то ![]() . Или, опуская значок X (но подразумевая его) запишем короче:
. Или, опуская значок X (но подразумевая его) запишем короче:
![]() (2.5)
(2.5)
Формула (2.5) представляет собой Правило вычисления производной (правило дифференцирования) сложной функции.
Собственно говоря, суть правила (2.5) проста. А именно, если функция ![]() – простая функция от X (из числа основных элементарных функций, чьи производные содержатся в таблице (2.1)), то ее производная и выглядит, и находится просто:
– простая функция от X (из числа основных элементарных функций, чьи производные содержатся в таблице (2.1)), то ее производная и выглядит, и находится просто: ![]() . А если
. А если ![]() , где
, где ![]() – две простых функции, то
– две простых функции, то ![]() – уже сложная функция от X. Ее производная
– уже сложная функция от X. Ее производная ![]() по X находится уже по формуле (2.5): сначала находим производную от функции
по X находится уже по формуле (2.5): сначала находим производную от функции ![]() по переменной U (точно так же, как находим производную от функции
по переменной U (точно так же, как находим производную от функции ![]() по переменной X), а затем умножаем ее на производную функции
по переменной X), а затем умножаем ее на производную функции ![]() по переменной X.
по переменной X.
Чтобы сделать наглядным применение этого правила, приведем таблицу сравнения, содержащую производные некоторых простых и аналогичных им сложных функций от X:
|
Производные простых функций (X – независимая переменная) |
Производные сложных функций ( Дифференцируемая функция) |
(2.6) |
|
1. |
1. | |
|
2. |
2. | |
|
3. |
3. | |
|
4. |
4. | |
|
5. |
5. | |
|
6. |
6. | |
|
(……) |
(……) |
Таблица (2.6) наглядно иллюстрирует разницу между производными простых и сложных функций.
Пример 8. ![]() ;
; ![]()

Пример 9. ![]() ;
; ![]()

Пример 10. ![]() ;
; ![]()
Решение.

Пример 11. ![]() ;
; ![]()
Решение.

 .
.
| < Предыдущая | Следующая > |
|---|