2.4. Выражение вектора на плоскости через координатные орты
Выражение вектора через его проекции
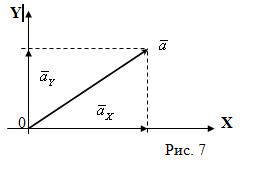
Пусть 
— проекция вектора 
на ось 
, 
— проекция вектора на ось 
(см. рис. 7). Очевидно, 
.
Линейные действия с проекциями
Утверждение 2. При сложении векторов, их проекции складываются.
Пусть векторы и 
выражаются через свои проекции:
, 
.
Тогда 
= (
)
().
Утверждение 3. При умножении вектора на число, его проекции также умножаются на это число.
Пусть . Тогда 
, где 
.
Координаты вектора в прямоугольной системе координат
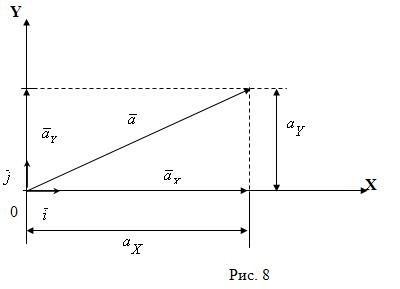
Единичные векторы 
и 
называются Координатными ортами: 
, 
; 
; 
; 
. Всякий вектор выражается через свои проекции: (см. рис. 8).
, 
(см. 2.3),
Где 
— модуль проекции .
, 
(см. 2.3),
Где 
— модуль проекции .
Выразим вектор через координатные орты: = + = 
+ 
,
Где коэффициенты , — Координаты вектора .
Определение 11. Координатами геометрического вектора в декартовой прямоугольной системе координат на плоскости называется пара чисел 
, определяемая следующим образом:
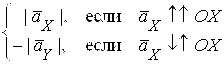, где 
— модуль проекции ,
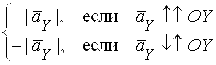, где 
— модуль проекции .
Утверждение 4. Любой вектор может быть представлен в виде линейной комбинации координатных ортов: = + . Коэффициенты этой линейной комбинации суть координаты вектора .
Обозначение: = {,}.
Пример 9. Вектор образует угол 
= 
с осью в декартовой прямоугольной системе координат на плоскости (см. рис. 9). Найти координаты вектора , если 
.
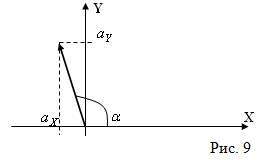
Решение. Имеем
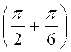= 3 
= 3
= 3
= 
= 
,
= 3 = 3 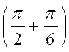= 3
= 3 = 
.
Таким образом, 
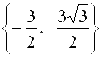или + .
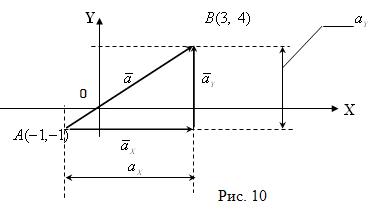
Пример 10. Пусть 
, 
. Найти координаты вектора 
(см. рис. 10).
Решение. Имеем 
{, }, где 
= 4 (
, 
);
= 5 (
, 
).
Таким образом, 
или = 4 + 5.
Пример 11. Пусть , . Найти модуль вектора .
А). Модуль вектора через длины его проекций:
=
=
=
, где 
, 
.
Б). Модуль вектора как расстояние между точками 
и 
:
=
=
=
.
Линейные действия над векторами в координатной форме
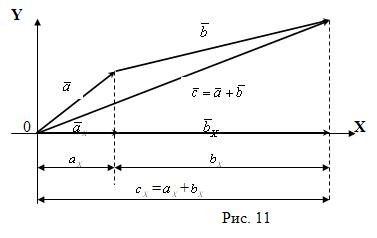
Утверждение 5. При сложении векторов их соответствующие координаты складываются.
Пусть = 
, = 
+ 
+ 
= ( + ) + ( + );
Или 
= 
, 
, 
(см. рис. 11).
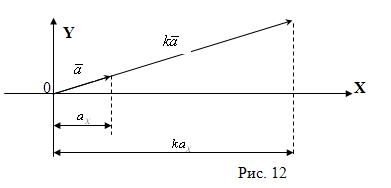
Утверждение 6. При умножении вектора на число, все его координаты умножаются на это число.
Пусть = +, или ={,}. Тогда = 
+ 
или = {, }, где 
(см. рис. 12).
Условие коллинеарности двух векторов на плоскости
Утверждение 7. Два вектора на плоскости коллинеарны тогда и только тогда, когда их координаты пропорциональны.
Например, если , причем вектор в раз длиннее вектора (т. е. 
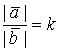), то . Тогда = + = = 
+
Или = , = . Отсюда получаем: 
= 
| < Предыдущая | Следующая > |
|---|
