1.2. Основные понятия теории дифференциальных уравнений

Дифференциальным уравнением называется уравнение, содержащее производные неизвестной функции.

Если в дифференциальном уравнении неизвестная функция является функцией одной независимой переменной, то оно называется Обыкновенным дифференциальным уравнением. Дифференциальное уравнение (1.1) представляет пример такого уравнения.

Если же входящая в дифференциальное уравнение неизвестная функция зависит от нескольких независимых аргументов, то оно называется Уравнением в частных производных. Примером служит уравнение

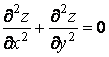, (1.2)

Которое содержит неизвестную функцию .

Порядком Дифференциального уравнения называется наибольший порядок входящей в уравнение производной. Так дифференциальные уравнения (1.1) и (1.2) – это уравнения второго порядка.

Решением Дифференциального уравнения называется функция, которая при подстановке в дифференциальное уравнение обращает его в тождество.

Например, легко проверить, что функция является решением дифференциального уравнения . Процесс решения дифференциального уравнения называется Интегрированием уравнения.

В дальнейшем рассматриваются лишь обыкновенные дифференциальные уравнения и их системы. Обыкновенное дифференциальное уравнение -го порядка

(1.3)

Содержит независимую переменную , неизвестную функцию и её производные , , …, .

График решения дифференциального уравнения Называется интегральной кривой. Уравнение считается проинтегрированным, если его решение найдено в явном виде или определяется неявно уравнением вида независимо от того, удается ли разрешить это уравнение относительно неизвестной функции или нет. Уравнение , которое определяет решение дифференциального уравнения, называется Интегралом этого дифференциального уравнения.

В данном пособии рассматриваются методы интегрирования и исследования дифференциальных уравнений первого порядка.

< Предыдущая		Следующая >