Примеры решения типовых задач по теории рядов
Задача 37. Найти область сходимости степенного ряда ![]()
Решение. Данный степенной ряд можно записать так:
![]() (1)
(1)
Применяем признак Даламбера:
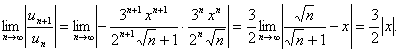
Как видно, ряд будет сходиться для тех значений Х, для которых
![]()
Выясним вопрос о сходимости ряда на концах интервала.
При ![]() ряд (1) примет вид
ряд (1) примет вид
![]() (2)
(2)
Ряд (2) является знакочередующимся; его общий член по абсолютному значению стремиться к нулю при N®¥. По признаку Лейбница о сходимости знакочередующихся рядов заключаем, что ряд (2) сходится. Следовательно, значение Х=-2/3 принадлежит области сходимости данного ряда.
Подставив в (1) Х=2/3, получим
![]() (3)
(3)
Ряд (3) расходится (для этого достаточно сравнить его с гармоническим рядом). Следовательно, значение Х=2/3 не принадлежит области сходимости данного ряда. Таким образом, ![]() - область сходимости исследуемого ряда.
- область сходимости исследуемого ряда.
Задача 38. Вычислить интеграл 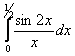 с точностью до 0,0001.
с точностью до 0,0001.
Решение. Предварительно представим подынтегральную функцию в виде степенного ряда. Используя известное разложение в степенной ряд функции Sinx, будем иметь
![]()
Тогда
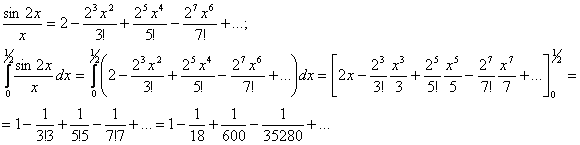
Мы получили знакочередующийся ряд, который удовлетворяет условиям теоремы Лейбница. Так как в полученном ряде четвертый член по абсолютному значению меньше 0,0001, то ограничиваемся только первыми тремя членами. Итак,
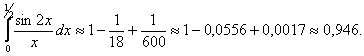
Задача 39. Разложить в ряд Фурье периодическую функцию F(X), заданную на интервале – периоде (-p, p):
![]()
Решение. Заданная функция F(X) удовлетворяет условиям разложения в ряд Фурье, поэтому имеем равенство
![]() (1)
(1)
Где An И Bn определяются по формулам
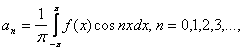 (2)
(2)
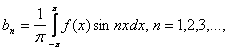 (3)
(3)
Положив в (2) N=0, получим коэффициент А0:
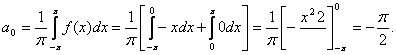
Используя формулу (2) и заданную функцию, имеем
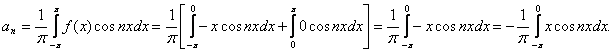
Интегрируя по частям, получаем
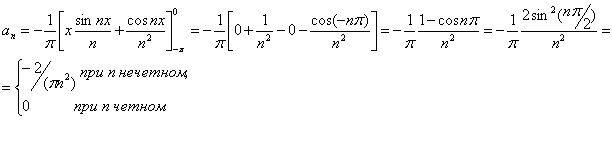
Определим коэффициенты Bn:
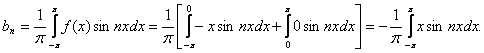
Интегрируя по частям, получаем
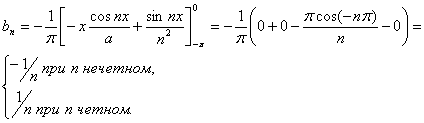
Подставляя найденные значения коэффициентов Фурье в (1), получаем
![]()
Задача 40. Функцию ![]() в интервале (0;p) разложить в ряд косинусов.
в интервале (0;p) разложить в ряд косинусов.
Решение. Так как по условию ряд заданной функции должен содержать только косинусы кратных дуг, то продолжим функцию в интервале (-p;0) четным образом. В результате будет получена четная функция, которая совпадает с заданной на интервале (0;p). Известно, что ряд Фурье для четной функции имеет вид
![]() (1)
(1)
Где
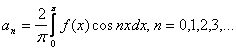 (2)
(2)
При N=0 получаем:
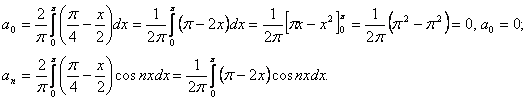
Интегрируем по частям:
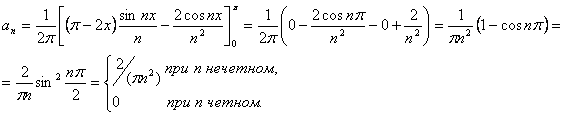
Подставив найденные значения коэффициента Фурье в (1), получим
![]()
| < Предыдущая | Следующая > |
|---|