4.1.1. Лабораторная работа 1. Статистическое оценивание параметров распределения
Основные теоретические положения изложены в разделе 3 Опорного конспекта данного пособия, а также в [ 2] , с.24-32, [3], гл.16, [6], с.126-138.
Целью работы является изучение методики статистического оценивания параметров закона распределения, освоение инструментов статистического анализа MS Excel.
Задача ставится следующим образом: случайная величина имеет закон распределения определенного вида, зависящий от параметра, значение которого неизвестно. Требуется на основании опытных данных оценить значение этого параметра.
Лабораторная работа состоит из двух частей. Первая часть включает в себя выполнение заданий 1 и 2 и представляет собой контрольный пример, решение которого приведено ниже. Во второй части самостоятельно выполняется индивидуальная работа, состоящая из заданий 3 и 4.
Порядок выполнения лабораторной работы
Задание 1
1.1. Получить с использованием Пакета анализа выборку объема ![]() из генеральной совокупности, в которой случайная величина ξ распределена по нормальному закону с параметрами
из генеральной совокупности, в которой случайная величина ξ распределена по нормальному закону с параметрами ![]() и σ=0,5.
и σ=0,5.
1.2. Найти точечные оценки математического ожидания, дисперсии, стандартного отклонения, а также стандартную ошибку оценки математического ожидания:
а) по данным малой выборки ![]() ;
;
Б) по данным большой выборки ![]() .
.
Задание 2
2.1. Найти доверительные интервалы, соответствующие доверительной вероятности β=0,95, для оценок математического ожидания, полученных в задании 1.2, Без использования MS Excel.
2.2. Выполнить задание 2.1 с использованием MS Excel.
2.3.Построить с использованием инструмента Описательная Статистика Пакета анализа статистический отчет для выборки малого объема.
Задание 3
3.1. При помощи Пакета анализа сМоделировать выборку случайной величины ξ, распределенной по нормальному закону с параметрами ![]() и σ. Значения параметров и объема выборки
и σ. Значения параметров и объема выборки ![]() следует выбрать в соответствии с последней цифрой шифра из табл. 4.1 (случайное рассеивание взять равным предпоследней цифре шифра).
следует выбрать в соответствии с последней цифрой шифра из табл. 4.1 (случайное рассеивание взять равным предпоследней цифре шифра).
Таблица 4.1
|
Послед-няя цифра шифра |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Σ |
1; 0,4 |
1; 0,5 |
2; 0,5 |
2; 0,4 |
3; 0,5 |
3; 0,6 |
5; 0,6 |
6; 0,7 |
7; 0,6 |
8; 0,7 |
|
|
42 |
44 |
46 |
48 |
50 |
49 |
47 |
45 |
43 |
41 |
3.2. Выполнить с использованием MS Excel точечное и интервальное оценивание математического ожидания генеральной совокупности по данным выборки, полученной в задании 3.1. Значение доверительной вероятности взять равным 0,90.
Задание 4 . По результатам выполнения заданий 1 и 2 сформулировать и обосновать выводы о том, как изменяется точность найденных параметров в зависимости от объема выборки.
Выполнение задания 1.1. Инструмент Генерация случайных чисел Пакета анализа предназначен для проведения статистического моделирования. Для моделирования выборки заданного закона распределения выполните следующие действия:
1. Выберите команду Сервис – Анализ данных. Откроется окно диалога “Анализ данных” (рис. 4.1).
2. Из списка инструментов анализа выберите Генерация случайных чисел и нажмите кнопку OK. На экране появится окно диалога “Генерация случайных чисел” (рис. 4.2).
3. Введите в поле Число переменных - 1 (поскольку требуется смоделировать один закон распределения), а в поле Число случайных чисел - 40 (объем выборки).
4. Закон распределения моделируемой случайной величины задается параметром Распределение: выберите из списка Нормальное. Откроется окно диалога для ввода параметров нормального распределения.
5. Введите в поле Среднее число 4, в поле ввода Стандартное отклонение - 0,5, а в поле Случайное рассеивание - число 4.
6. В разделе “Параметры вывода” установите переключатель Выходной интервал. В одноименном поле укажите адрес ячейки $А$6, начиная с которой будут выводиться на экран выборочные значения.
7. Нажмите кнопку OK. В столбце А, начиная с ячейки А6, появятся генерируемые значения выборки.
8. Значения ячеек А26:A45 перенесите в ячейки B6:B25 для удобства дальнейшей обработки.
Создаваемая электронная таблица представлена в таблице 4.2 в режиме формул и в таблице 4.3 в режиме вычислений.
Завершая выполнение первого задания, оформите таблицу так, как указано:
Ячейка Значение
B1 ТОЧЕЧНОЕ И ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
A2 выборка из нормального распределения с параметрами
Ячейка Значение Ячейка Значение
F2 мат. ожид. G2 4
F3 станд. откл. G3 0,5
F4 дов. вер. G4 0,95
F5 объем выборки G5 40
Назовите ярлык рабочего листа Оценки.
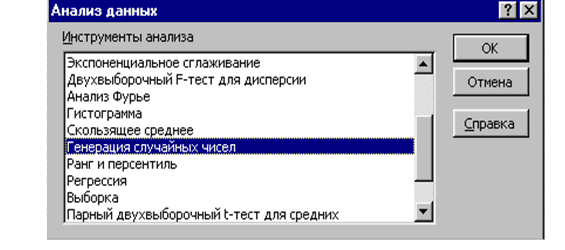
Рис. 4.1. Окно диалога «Анализ данных»

Рис. 4.2. Окно диалога «Генерация случайных чисел»
В табл. 4.2 приводится текст программы в Excel (режим показа формул) выполнения задания 1.1; в табл. 4.3 – программа в режиме вычислений.
Программа в режиме вычислений:
Таблица 4.3

Выполнение задания 1.2. Для нахождения значений точечных оценок воспользуемся функциями, которые содержатся в категории Статистические. Функция СРЗНАЧ возвращает значение оценки математического ожидания, вычисленное по формуле  . (4.1)
. (4.1)
Выборочная дисперсия 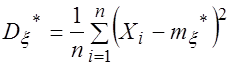 (4.2)
(4.2)
Является смещенной оценкой дисперсии генеральной совокупности. Несмещенной и состоятельной оценкой дисперсии является величина 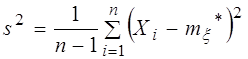 . (4.3) Функции ДИСПР и СТАНДОТКЛОНП – значения выборочной дисперсии и стандартного отклонения. Для вычисления значений несмещенной оценки дисперсии и оценки стандартного отклонения воспользуемся функциями ДИСП и СТАНДОТКЛОН соответственно.
. (4.3) Функции ДИСПР и СТАНДОТКЛОНП – значения выборочной дисперсии и стандартного отклонения. Для вычисления значений несмещенной оценки дисперсии и оценки стандартного отклонения воспользуемся функциями ДИСП и СТАНДОТКЛОН соответственно.
Введите формулы для вычисления значений точечных оценок параметров закона распределения для малой выборки в строку 8 (ячейки D8:H8), для большой выборки – в строку 9 (ячейки D9:H9).
Ячейка Значение
D8 =СРЗНАЧ(A6:A25)
D9 = СРЗНАЧ(A6:B25)
E8 =ДИСП(A6:A25)
E9 =ДИСП(A6:B25)
F8 =СТАНДОТКЛОН(A6:A25)
F9 = СТАНДОТКЛОН(A6:B25)
G8 =ДИСПР(A6:A25)
G9 =ДИСПР(A6:B25)
H8 =СТАНДОТКЛОН(A6:A25)
H9 = СТАНДОТКЛОН(A6:B25)
В ячейках С8 и С9 укажите объемы большой и малой выборок – числа 20 и 40.
В ячейках I8 и I9 наберите формулу для расчета стандартной ошибки
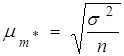 .
.
Ячейка Значение
I8 =F8/КОРЕНЬ(С8)
I9 =F9/КОРЕНЬ(С9)
Чтобы электронная таблица была удобной для анализа результатов ычислений, введите следующие поясняющие заголовки:
Ячейка Значение Ячейка Значение
D6 ТОЧЕЧНЫЕ ОЦЕНКИ С7 Объем выб.
D7 Выб. среднее E7 Несм. дисп.
F7 Несм. станд. откл. G7 Выб. дисп.
Н7 Выб. станд. откл. I7 Станд. ошибка
Выполнение задания 2.1. Задача о нахождении доверительного интервала для математического ожидания нормально распределенной случайной величины решена в Примере3.3. В расчетах следует использовать вычисленные при выполнении задания 1.2 значения точечных оценок математического ожидания и дисперсии.
Выполнение задания 2.2.
1. Доверительный интервал для математического ожидания в случае малой выборки определяется по формуле
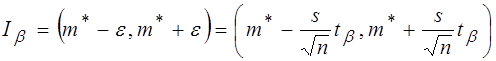 .
.
Расчет выполняется в ячейках C13:G13.
1.1. Введите значения объемов малой и большой выборок (числа 20 и 40) в ячейки C13 и C14 соответственно.
1.2. Функция СТЬЮДРАСПОБР возвращает квантиль порядка ![]() распределения Стьюдента с
распределения Стьюдента с ![]() степенью свободы
степенью свободы ![]() . В качестве аргументов функции следует указать уровень значимости α=1 – β и число степеней свободы. Введите в ячейку D13 формулу
. В качестве аргументов функции следует указать уровень значимости α=1 – β и число степеней свободы. Введите в ячейку D13 формулу
=СТЬЮДРАСПОБР(1-$G$4;C13-1).
1.3. Для вычисления предельной ошибки 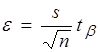 введите в ячейку E13 формулу =D13*F8/КОРЕНЬ(С13).
введите в ячейку E13 формулу =D13*F8/КОРЕНЬ(С13).
1.4. Нижнюю и верхнюю границы доверительного интервала вычислите в ячейках F13 и G13.
Ячейка Значение
F13 =D8-E13
G13 =D8+E13
2. Расчет границ доверительного интервала для математического ожидания большой выборки по формуле (3.3) выполните в ячейках D14:G14. Для нахождения квантили нормального стандартного распределения порядка (1+β)/2 воспользуйтесь функцией НОРМСТОБР. Введите следующие формулы:
Ячейка Значение
D14 = НОРМСТОБР((1+$G$4)/2)
E14 = D14*F9/КОРЕНЬ(C14)
F14 = D9-E14
G14 = D9+E14
Введите комментарий так, как указано ниже.
Ячейка Значение
D11 ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ
Ячейка Значение Ячейка Значение
С12 объем. выб. D12 квантиль
E12 пред. ошибка F12 ниж. гран.
G12 верх. гран.
3. Функция ДОВЕРИТ возвращает предельную ошибку для заданной доверительной вероятности. Аргументами этой функции являются уровень значимости, несмещенное стандартное отклонение и объем выборки. Введите в ячейку E15 формулу
=ДОВЕРИТ(1-$G$4;F9;C14).
Убедитесь в том, что значения в ячейках E14 и E15 совпадают.
Выполнение задания 2.3. Инструмент Описательная статистика позволяет построить статистический отчет для входных данных (заданной выборки). Выходная таблица содержит два столбца: левый столбец содержит названия статистических данных, правый – статистические данные.
Для получения результатов обработки выборки в выходной таблице выполните следующие действия:
1. Выберите команду Сервис–Анализ данных – Описательная статистика.
2. В открывшемся окне диалога “Описательная статистика” Задайте параметры. Введите входной интервал $A$6:$A$25. Для параметра Группирование установите переключатель По столбцам.
3. Установите флажки Итоговая статистика, Уровень надежности, В одноименное поле введите 95 %.
4. В разделе Параметры вывода установите переключатель Выходной интервал и в поле Выходной интервал введите адрес ячейки $D$17.
5. Параметры окна диалога “Описательная статистика” установлены. Нажмите кнопку OK. На экране появится таблица, созданная инструментом Описательная статистика для заданной выборки.
Рассмотрите внимательно эту таблицу. Сравните приведенные в ней значения для среднего, дисперсии и стандартного отклонения малой выборки, а также стандартной ошибки с результатами расчетов тех же величин с использованием формул (со значениями в ячейках D8, E8, F8, I8). Уровнем надежности в таблице названа предельная ошибка.
В таблице приведены и другие характеристики выборки. Медианой Называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Интервалом названа разность между наибольшим и наименьшим значениями выборки. Максимум – это наибольший элемент выборки, а Сумма и счет – это сумма значений элементов выборки и ее объем.
Подготовить отчет по выполнению работы:
1. Название работы и задание.
2. Результаты ручного счета по заданию 2.1.
3. Две распечатки таблицы, созданной при выполнении задания 3 (одна содержит результаты вычислений, другая - сами формулы).
4. Результаты анализа данных по заданию 4.
| < Предыдущая | Следующая > |
|---|